Find the centroid of the region in the first quadrant bounded by the xaxis, the parabola y^2 = 2x, and the line x y = 4 I've graphed the function, and it looks like a triangle with one side curved (the parabola)Parabola Normals are drawn at points P, Q and R lying on the parabola y2 = 4x which intersect at (3, 0) Then, List 1 Area of ΔP QR Radius of the circum circle of ΔP QR Distance of the vertex from the centroid of ΔP QR Distance of the centroid from the circumcentre of ΔP QR List 2 2 25 Centroid of parabola Thread starter Jbreezy;
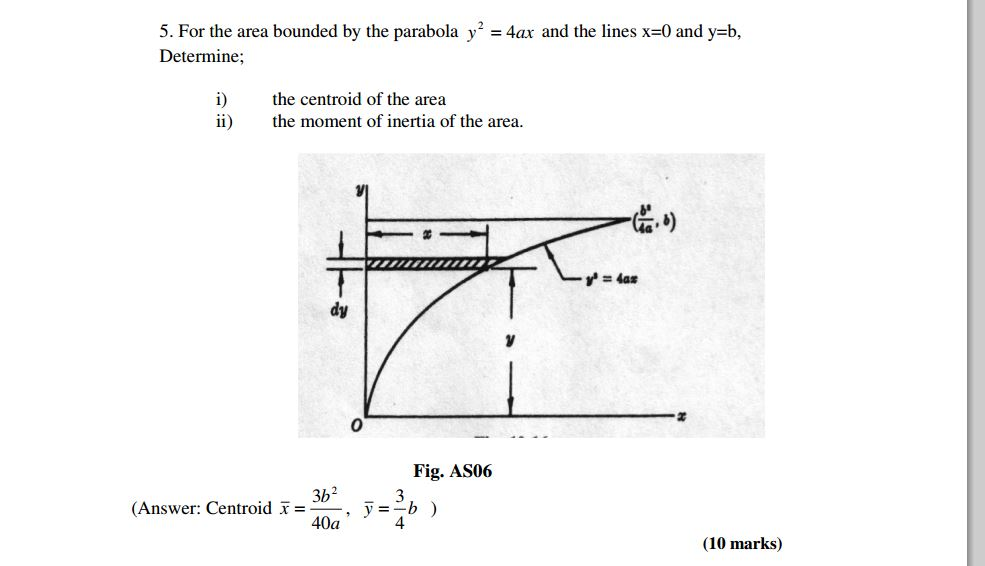
5 For The Area Bounded By The Parabola Y 2 4ax And Chegg Com
Centroid of parabola y=x^2
Centroid of parabola y=x^2-Solve for x math2x = y^2 2y 3/math Find where the yintercepts let x = 0, mathy^2 2y 3 = 0/math, therefore mathy = 3/math and mathy = 1 /mCalculus questions and answers Find The Centroid Of The Region Bounded By The Line Y = 1 And The Parabola Y = X^2




Centroid Of Area By Integration Spr18 Youtube
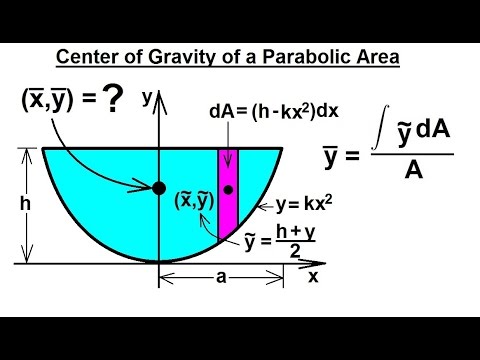
We get $\dfrac{\pi b^2}{2}$ For the height of the centroid, you need to find the moment of the paraboloid about the $x$$y$ plane The crosssectional area at height $z$ is $\pi(x^2y^2)=\pi z$ A thin slice of thickness $dz$ at that height has approximate volume $\pi z\,dz$, and therefore moment about the $x$$y$ plane approximately $z(\pi z \,dz)$$y^2 = \dfrac{b^2}{a}x$ → equation of parabola $y = \dfrac{b}{a^{1/2}}x^{1/2}$ Differential area $dA = y \, dx$ $dA = \dfrac{b}{a^{1/2}}x^{1/2} \, dx$ Area of parabola by integration $\displaystyle A = \int_0^a \left( \dfrac{b}{a^{1/2}}x^{1/2} \right) \, dx$ $\displaystyle A = \dfrac{b}{a^{1/2}}\int_0^a x^{1/2} \, dx$ $A = \dfrac{b}{a^{1/2}}\left \dfrac{x^{3/2}}{3/2} \right_0^a$ Show transcribed image text Calculate the centroid of the region beneath the parabola y = x^2 and above the xaxis where x is in the interval 0,3 Assume uniform density Please sketch Calculate the centroid of the region beneath the parabola y = x^2 and above the xaxis where x is in the interval 0,3
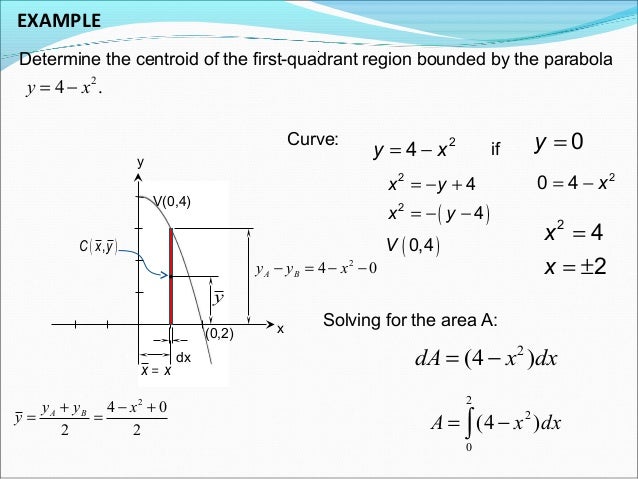
Find the centroid of the area bounded by the parabola y = 4 x2 and the xaxis a (0,19) b (0,18) c (0,16) d (0,17)Solution for ) Find the centroid of the first quadrant area bounded by the parabola y = x2 and the line y = x a (1/3, 3/4) %3D b (1/3, 3/4) c (1/2, 2/5) Answered )(x0) 2 (yp) 2 = (yp) 2 (xx) 2 x 2 (yp) 2 = (yp) 2 If we expand all the terms and simplify, we obtain x 2 = 4py Although we implied that p was positive in deriving the formula, things work exactly the same if p were negative That is if the focus lies on the negative y axis and the directrix lies above the x axis the equation of the
Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceFinding a centroid The area of the region in the first quadrant bounded by the parabola y=6 xx^{2} and the line y=x is 125/ 6 square units Find the centroidFind (x, y), centroid of the region of constant density k covering the region bounded by the parabola y = 2x x^2 and the line y = 2x Get more help from Chegg Solve it with our calculus problem solver and calculator




Centroid Definition Properties Theorem And Formulas




Mechanical Engineering Centroids Center Of Gravity 10 Of 35 C G Of A Parabolic Spandrel Youtube
This equation computes the x and y components of the Centroid for an nth degree parabola, convex up, where the equation for the parabola is y = ( h b1 n)x1 n ( h b 1 n) x 1 n The Centroid ( C) represents center of mass of the parabola The Centroid has x & y units of length representing a coordinateThis engineering statics tutorial goes over how to find the centroid of the area under a parabola It requires a simple integrationIf you found this video h Centroid In polar coordinates $r = \sqrt{{\bar{x}}^2 {\bar{y}}^2} = \sqrt{(04a)^2 a^2}$ $r = \frac{\sqrt{29}}{5}a = 1077a$ $\theta = \arctan \left( \dfrac{\bar{y}}{\bar{x}} \right) = \arctan \left( \dfrac{a}{04a} \right)$ $\theta = ^\circ$ Centroid




Calculus Ii Lesson 7a Applications Of Integration 6 Centroids Application Center



6 6 Moments And Centers Of Mass Calculus Volume 1
Show transcribed image text Find the centroid of an area bounded by the parabola y = 4 – x^2 and the line y = x – 2 Find the arc length of the graph y = x^3/6 1/2x on the interval (1/2, 2) Find the centroid of an area bounded by the parabola y Locate the centroid of the plane area bounded by the equation y^2 = 4x, x = 1 and the xaxis on the first quadrant Problem Answer The coordinates of the center of the plane area bounded by the parabola, the line and the xaxis of the first quadrant is at (3/5, 3/4) The centroid of a parabola is found with the equation y = h/b^2 * x^2, where the line y = h Additionally, the area is 4bh/3
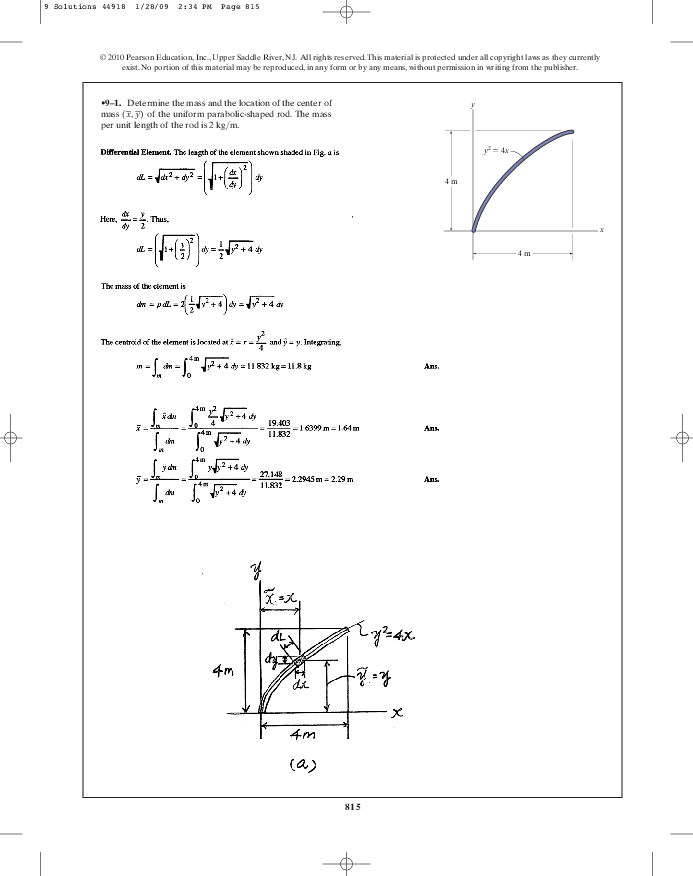



Pdf Chapter 9 Rafey Imtiaz Academia Edu



Http Www Rpi Edu Dept Core Eng Www Iea F15 Lectures Lecture17 Pdf
(viii) The combined equation of the pair of tangents drawn from a point to a parabola y 2 = 4ax is given by SS 1 = T 2 where, S = y 2 – 4ax, S 1 = y 1 2 – 4ax 1 and T = yy 1 – 2a (x x 1) Important Results on Tangents The tangent at any point on a parabola bisects the angle between the focal distance of the point and the perpendicular on the directrix from the pointFind the area of the region enclosed by the parabola x^2 = y, the line y = x 2 and the x axisclass 12 maths ncert solutions,maths class 12 ncert soluti 1021 rows The following is a list of centroids of various twodimensional and threedimensional objects The centroid of an object X {\displaystyle X} in n {\displaystyle n} dimensional space is the intersection of all hyperplanes that divide X {\displaystyle X} into two parts of equal moment about the hyperplane Informally, it is the "average" of all points of X {\displaystyle X} For an object of uniform composition, the centroid
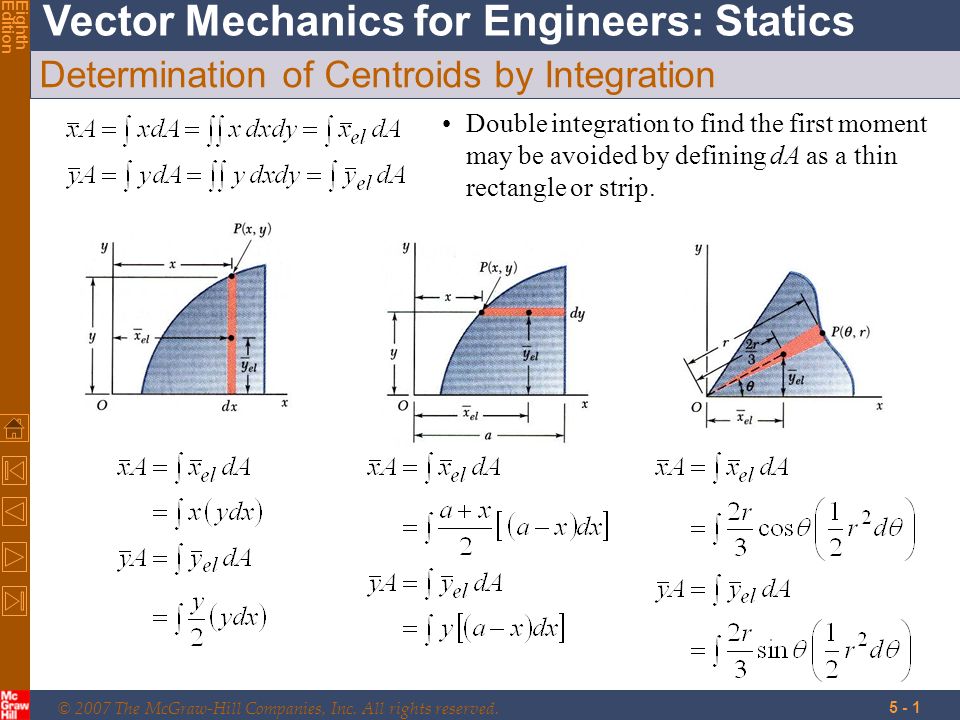



Determination Of Centroids By Integration Ppt Video Online Download




First Moments And Centroids Mcgraw Hill Education Access Engineering
Find the centroid of the region bounded by the curve x=2y^2 and the yaxis my work is shown below A= integral of (2y^2)dy from 0 to 1 M_y= (1/2) integral of (2y^2)^2 dy from 0 to 1 M_x= integral of (y)(2y^2)dy from 0 to 1 x= (M_y)/A y= (M_x)/A centroid is (x,y) I'm sure I may have made some mistakes in my integration set up for A,M_x,M_y please helpShow that the coordinates of the centroid G of the area between the parabola y = \frac{x^2}{a} and the straight line y = x are \overline{x} = \frac{a}{2} , \overline{y} = \frac{2 a}{5}Showing a representative strip 2 Form the product of the area of the rectangle and the distance of its centroid from the axis 4 For a plane region having an area A, centroid and moments and with respect to x and y axes, ( ),, yxC xM yM yM Ax= xM Ay=and A M x y = A M y x = 5




Centroid Of Volume Bounded By A Line And A Parabola Mathematics Stack Exchange




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts
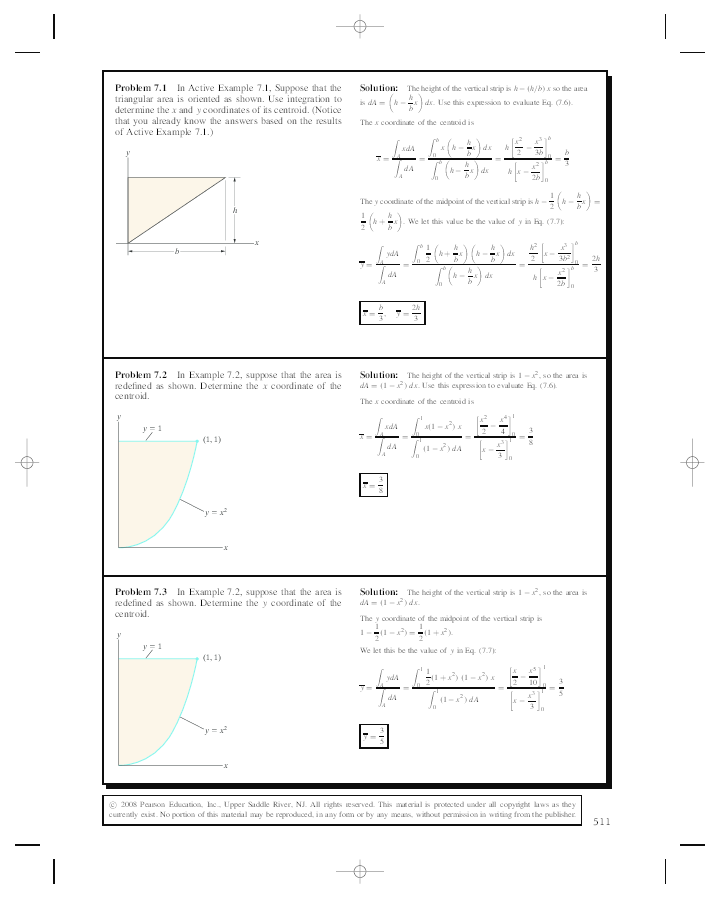
The equations of the parabolas are The centroid of the region has coordinates It can be found using , where is the coordinates of the centroid of the differential element of area dA Use differential elements consisting of rectangular vertical slices of width dx and height yThis means that variable x will be the variable of integration In this case, and Show transcribed image text Find the centroid of the thin plate bounded by the line y = I and the parabola y = x^2 Find the centroid of the thin plate bounded by the line y = I and the parabola y = x^2Y^2=4x (Area) Please show a graph or illustration and explain thoroughlyThank you enotes "NEED BADLY"' and find homework



Solved 1 How Far From The X Axis Is The Centroid Of The Area Bounded By The Curves X 2 36y The X Axis And The Line X 12 Provide Complete Course Hero



Pappus S Theorem
Centroid Of Parabola Y X 2 ekonomická univerzita banská bystrica etický kódex štátneho zamestnanca elektronicky listok na vlak europska liga 17 18 europa staty a hlavne mesta elektronická prihláška na vš elektronická učebnica pedagogického výskumu elán voda čo ma drží nad vodou akordy eva vôňa roka 17 embraco spišská nová vesFind the centroid of the portion between the parabola y=x^2 and y=x Find the centroid of the portion between the parabola y=x^2 and y=x Find the centroid of the portion between the parabola y=x^2 and y=x A professional Academic Services Provider Platinum Essays, We are Built on the Values of Reliability, Proffessionalism, and IntegrityA xcentroid or a ycentroid referring to the coordinate along that axis where the centroidal axis intersects the coordinate axis 5 Centroids by Integration Centroidal Axis 6 Centroids by Integration Wednesday, 4 Wednesday, Centroids !




Solved X 2 A Y B Y Locate The Centroid Of The Parabolic Area X 2 A Y B 1 Answer Transtutors
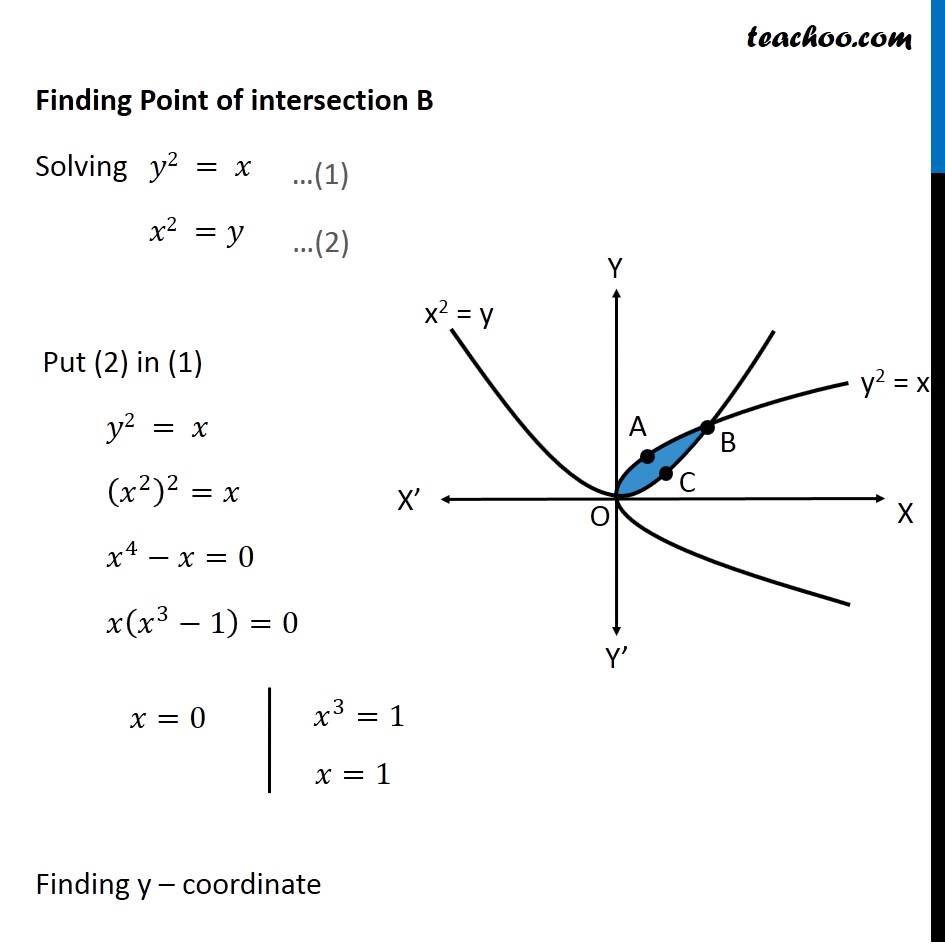



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X
Three normal are drawn from point (5, 0) to parabola y^2 = 4x The centroid of the triangle formed by feet of these three normals is maths Asked on by Bablu Nagar Three normal are drawn from point (5,0) to parabola y2 = 4xFind the coordinates of the centroid of the plane area bounded by the parabola y = 4 – x^2 and the xaxis Contribute to PinoyBIX Community either by Asking question or Answering then Share it to Social Media!!!Correct answers 1 question Urgent!
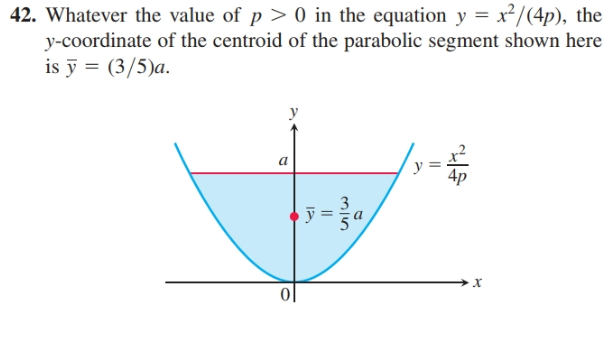



Answered 42 Whatever The Value Of P 0 In The Bartleby




How To Find Centroid Of A Parabolic Spandrel By Integration Youtube
Centroid calculator parabola Centroid of area by integration duration The centroid of an object in dimensional space is the intersection of all hyperplanes that divide into two parts of equal moment about the hyperplane Your function is y 16 x 2 or equivalently x 16 y The straight line is always a tangent to the parabola y 2 = 4ax for any value of m The coordinates of point of contact are Thus, ycoordinate of the centroid becomes Hence the centroid lies on the xaxis, ie axis of the parabola If three normals drawn to any parabolas y 2 = 4ax from a given point (h, k) be real Then h > 2a 1 Sketch the region;



5 Centroid Of An Area By Integration




Solution Find The Coordinates Of The Centroid Of The Plane Area Bounded By The Parabola And X Axis
Question What is the area bounded by the parabola y^22x2y3 =0 and the yaxis? Find the centroid of the area bounded by the parabola y=4x^2 and the xaxis A(0,16) B(0,17) C(0,18) D(0,19) CALCULUS Sketch the region enclosed by the given curves y = 4/X y = 16x, y = 1X/16 x > 0 and the area between the curves MathFind the area of the region bounded by y 2 = 9x, x = 2, x = 4 and the xaxis in the first quadrant The equation of curve is y 2 = 9x, which is right handed parabola Two lines are x = 2, x = 4



1
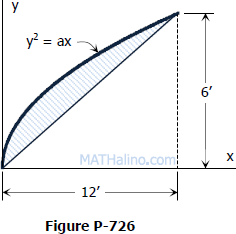



726 Area Enclosed By Parabola And Straigh Line Centroid Of Composite Area Engineering Mechanics Review At Mathalino
Centroid of parabola y=x^2Solution Find the coordinates of the centroid of the plane area bounded by the parabola and xaxis Solution Locate the centroid of the plane area bounded by y = x^2 and y = x Solution Find the area of the curve r^2 = a^2 cos 2θA 6 0 unit2 B 8 300 unit2 C 5 600 unit2 D 6 400 unit2 Part 2 What is the moment of inertiaThe simplest equation of a parabola is y 2 = x when the directrix is parallel to the yaxis In general, if the directrix is parallel to the yaxis in the standard equation of a parabola is given as y2 = 4ax If the parabola is sideways ie, the directrix is parallel to xaxis, the standard equation of a parabole becomes, x2 = 4ayAnswer to Find the centroid of the region bounded by the line y=x and the parabola y = x^2 By signing up, you'll get thousands of stepbystep for Teachers for Schools for Working Scholars




How To Find The Centroid Of The Area Under A Parabola Youtube




Finding The Centroid Of The Planar Region Bounded By The Parabola Y 4 X 2 And The Line Y X 2 Study Com
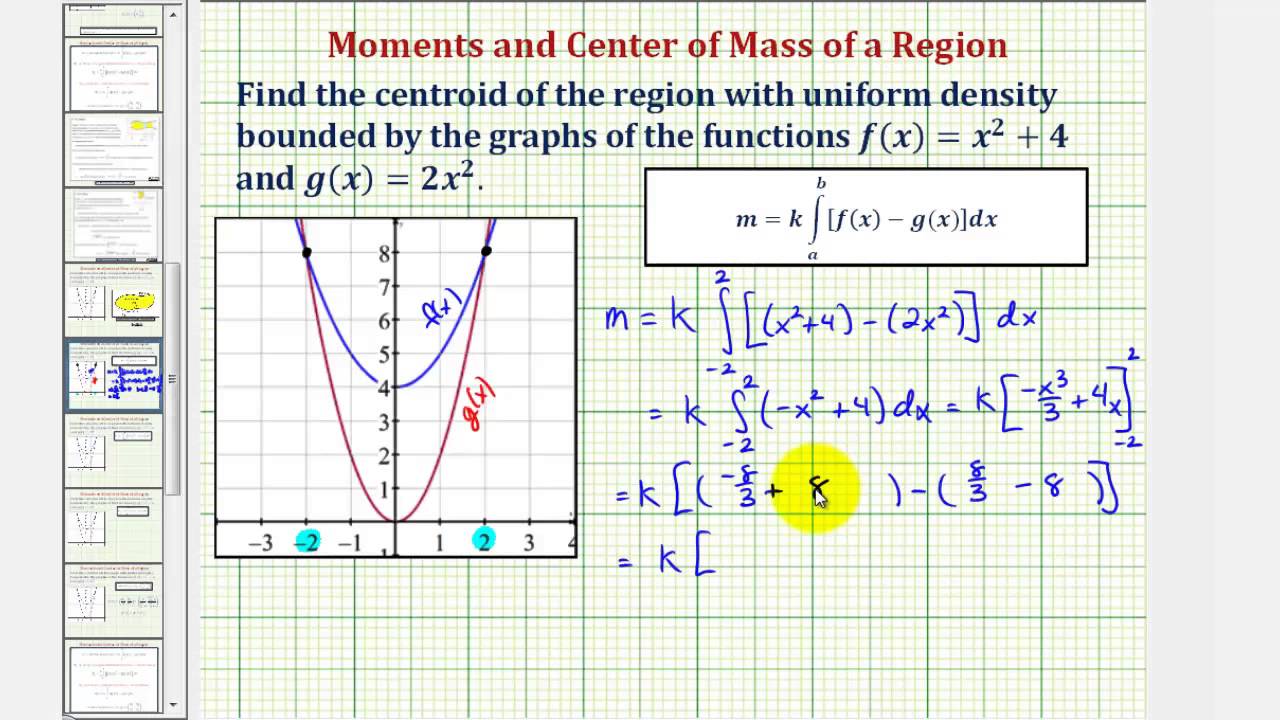
#1 Jbreezy 5 0 Homework Statement y = 16 x^2 find centroid bounded by x axis Homework Equations x = (1/A) ∫ x(f(x)) dx and (1/A) (1/2)(f(x))^2 dx = y The Attempt at a Solution I just applied it It is a weird because I would of thought that x would of beenThe coordinates of the center of mass ( x ^, y ^) is ( x ^, y ^) = ( 1 A ∫ a b x ( f ( x) − g ( x)) d x, 1 2 A ∫ a b ( f 2 ( x) − g 2 ( x)) d x) where A = ∫ a b f ( x) − g ( x) d x Take f ( x) = 4 and g ( x) = x 2 x ^ = 3 32 ∫ − 2 2 x ( 4 − x 2) d x = 0 y ^ = 3 64 ∫ − 2 2 ( 16 − x 4) d x = 12 5 so Get an answer for 'Find the centroid of the area bounded byx^2=4y ;




Lesson 12 Centroid Of An Area
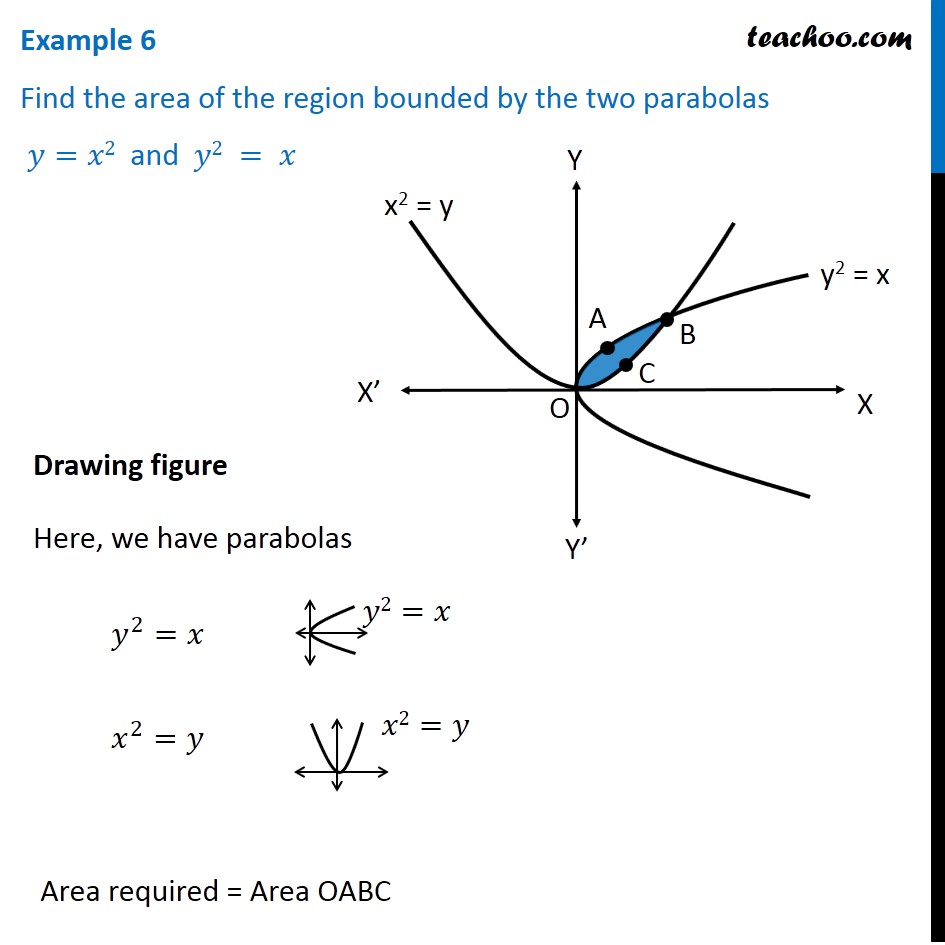



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X
Find the centroid of the region in the first quadrant bounded by the x axis, the parabola y^{2}=2 x, and the line xy=4 💬 👋 We're always here Join our Discord to connect with other students 24/7, any time, night or dayGiven the region beneath the parabola {eq}y = 9 x^2 {/eq} and above the {eq}x {/eq}axis In order to find the centroid, we must first find See full answer belowFind the center of mass of a thin plate covering the region bounded above by the parabola y = 4 x 2 and below by the xaxis Assume the density of the plate at the point (x,y) is δ = 2x 2, which is twice the square of the distance from the point to the yaxis Show Video Lesson



Http Faculty Mercer Edu Jenkins He Documents Centroids Pdf




Calculus Ii Lesson 7a Applications Of Integration 6 Centroids Application Center
Centroid for Cshapes John Ray Cuevas Area 1 x = 6000 millimeters y = 00 millimeters Area 2 x = millimeters y = 6500 millimeters Area 3 x = 60 millimeters y = 110 millimeters d Solve for the Ax values Multiply the area of each region by the distances from the yaxis MBBS MRCPsych PGDip Home; Find the coordinates of the centroid of the plane area bounded by the parabola y = 4 – x^2 and the xaxis Problem Answer The coordinates of the center of the plane area bounded by the parabola and xaxis is at (0, 16)




Centroid Triangle Physical Quantities
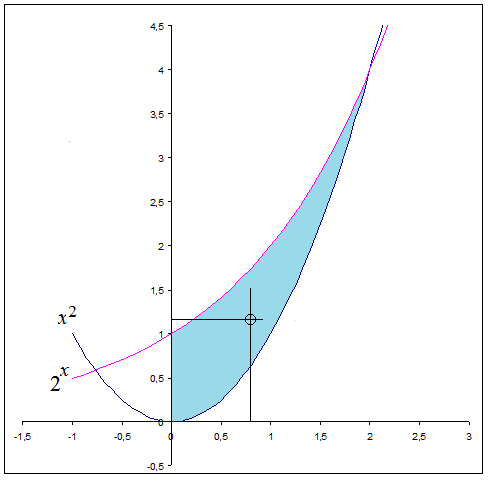



Find Centroid Of Region Of Two Curves Mathematics Stack Exchange
2 > @ y > a x dx@ yA y dA a x dx a x •Evaluate the centroid coordinates 3 4 ab a 2b x xA Q y x a 4 3 3 10 ab ab 2 y yA Q x y b 10 3 5 22 Theorems of PappusGuldinus •Surface of revolution is generated by rotating a plane curve about a fixed axis •Area of a surface of revolution is



Whatever The Value Of P 0 In The Equation Y Chegg Com
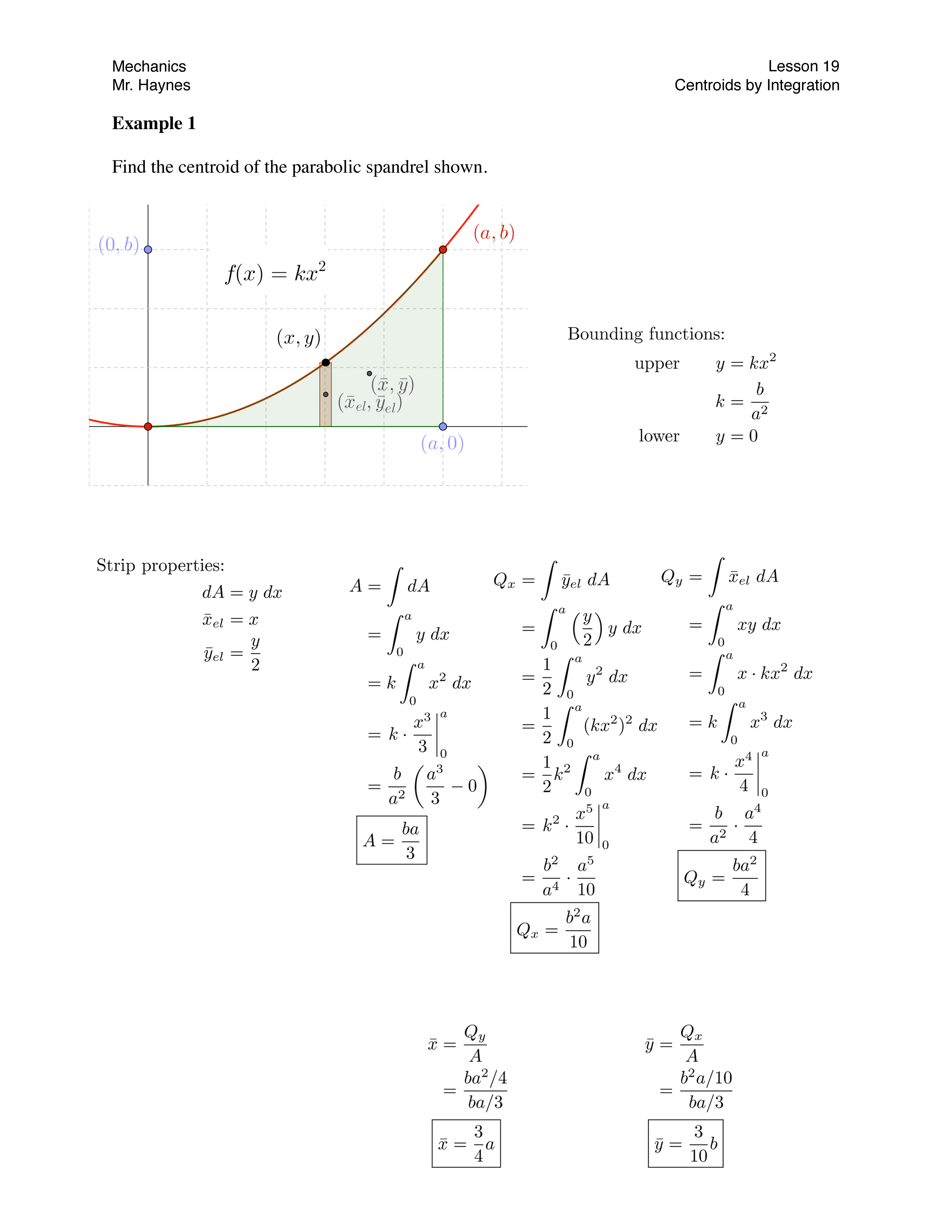



Determination Of Centroids By Integration




Centroid Of Area By Integration Spr18 Youtube




Ch09h Problem 9 16 Locate The Centroid Of The Shaded Area Bounded By The Parabola And The Line Y A Solution 3 A A 0 2 2 Xc 2 2 A 3 A 2 A 1 3 A Y Course Hero
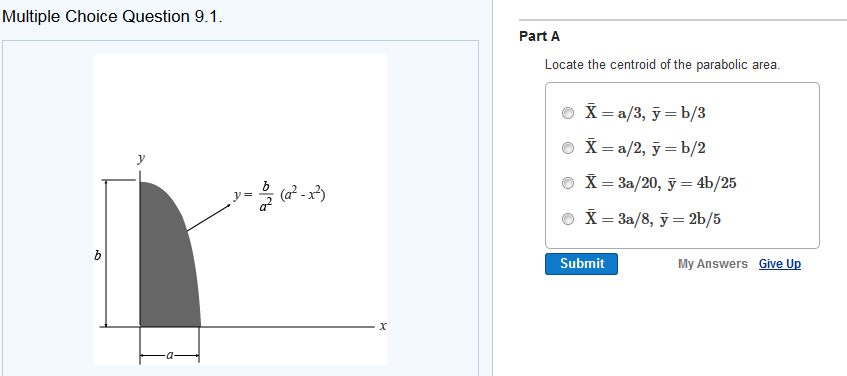



Locate The Centroid Of The Parabolic Area Chegg Com
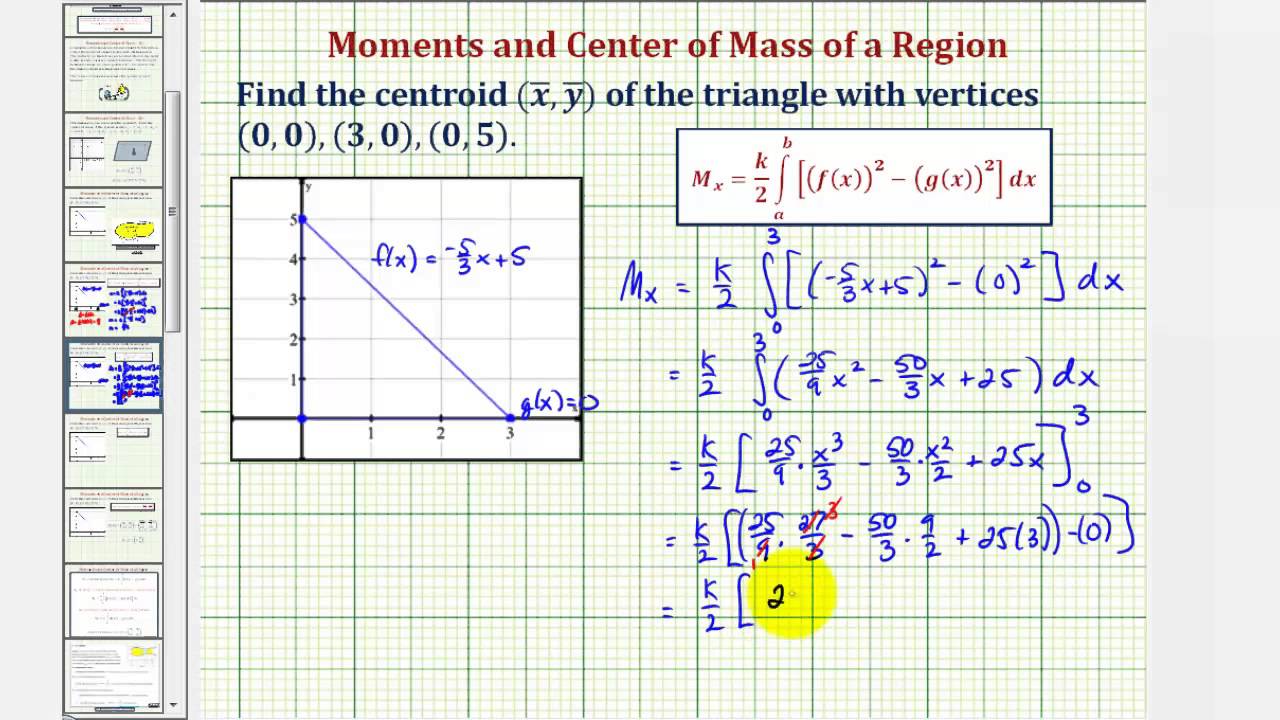



Calculate The Centroid Or Center Of Mass Of A Region Video Lessons Examples Step By Step Solutions




Engineering Mechanics Statics Ppt Download



Center Of Mass And Moments




Centroid Definition Properties Theorem And Formulas
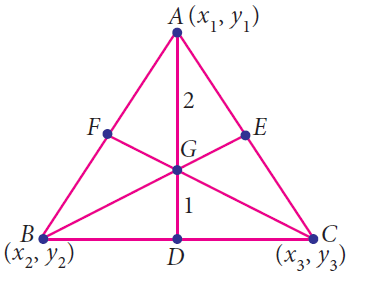



Find The Coordinates Of The Centroid Of A Triangle With Vertices
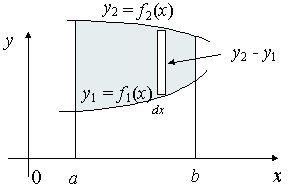



5 Centroid Of An Area By Integration



Http Www Rpi Edu Dept Core Eng Www Iea F15 Lectures Lecture17 Pdf




Solved Locate The Centroid Of The Shaded Area Bounded By The Locate The 1 Answer Transtutors




1 Find The Mass And Centroid Of The Region Bounded By The Y2 With P Homeworklib
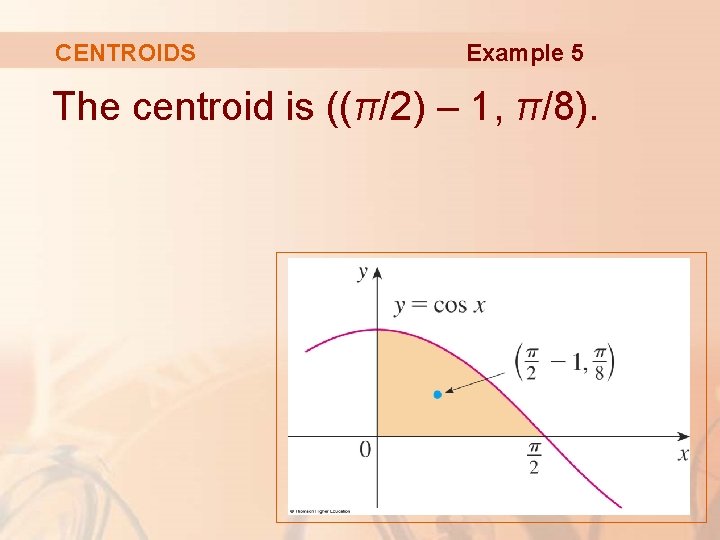



8 Further Applications Of Integration Further Applications Of
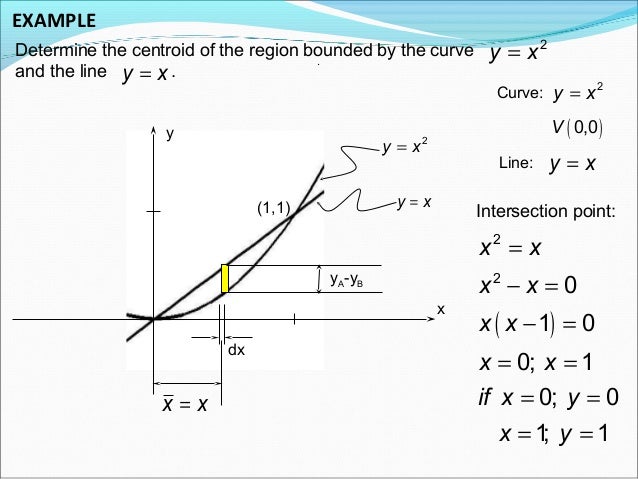



Lesson 12 Centroid Of An Area



Pappus S Theorem



Centroid Of Plane Body 8 Sideway Output To



What Is The Centroid Of The Solid Formed By Revolving The Region Bounded By Y 4 X 2 And Y X And X 0 About Y Axis Quora




Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com




Find The Coordinates Of The Centroid Of The Plane Gauthmath



Mechanics Map Centroid Of An Area



Anvari Net Dynamics Chapter 9 Pdf




Mechanics Map Centroid Of An Area



Http Www Iitg Ac In Rkbc Me101 Presentation L16 18 Pdf



Http Www Iitg Ac In Rkbc Me101 Presentation L16 18 Pdf



1
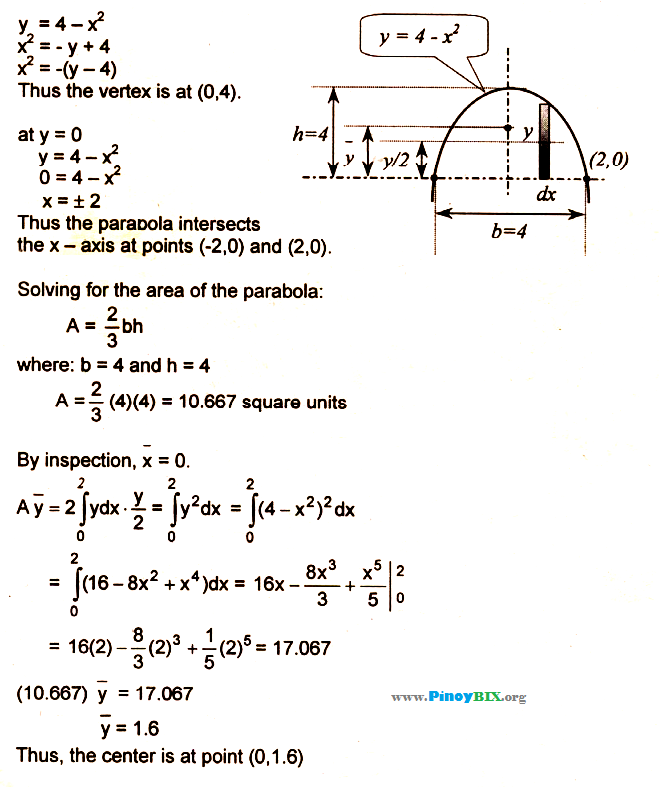



Solution Find The Coordinates Of The Centroid Of The Plane Area Bounded By The Parabola And



How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic
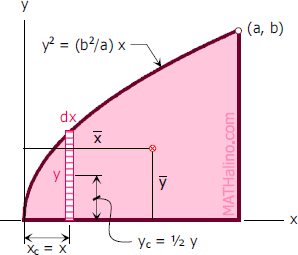



705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino




Centroid Area Moments Of Inertia Polar Moments Of Inertia Radius Of Gyration For The First Quadrant Of A Parabolic Area




Determine The Centroid X Y Of The Shaded Area Youtube




Locate The Centroid X Bar Of The Parabolic Area Chegg Com
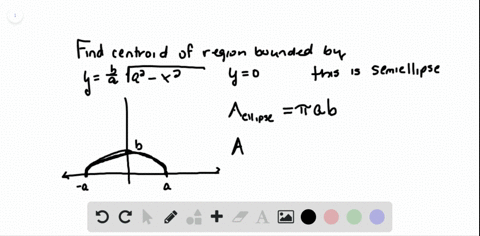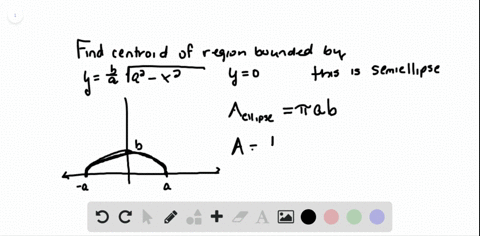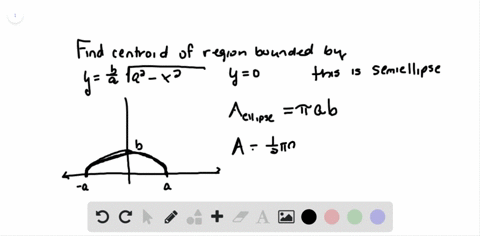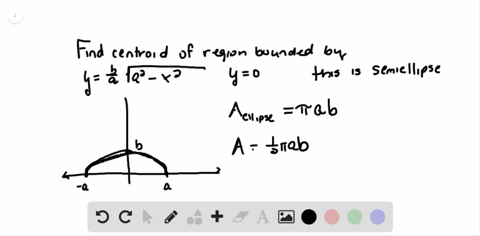



Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2



Q Tbn And9gcsjguchjp5puxk4qa Q1k5eh2jsixmfflxsbiljafdna63uvwkp Usqp Cau




Lesson 12 Centroid Of An Area




List Of Centroids Wikipedia



1



5 Centroid Of An Area By Integration




Calculate The Centroid Or Center Of Mass Of A Region Video Lessons Examples Step By Step Solutions




Mechanical Engineering Centroids Center Of Gravity 11 Of 35 C G Of A General Spandrel 1 Youtube




5 For The Area Bounded By The Parabola Y 2 4ax And Chegg Com



Mechanical Engineering Centroids Center Of Gravity 9 Of 35 C G Of A Parabolic Area Youtube




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora




List Of Centroids Wikipedia



5 Centroid Of An Area By Integration




Find The Center Of Gravity Centroid Of The Region R Enclosed Between The Curves Y X 2 And Y X 6 Study Com




Solution Locate The Centroid Of The Plane Area Bounded By The Parabola The Line And The X Axis




Determine The Coordinates Of The Centroid Of The Area That Lies Between The Straight Line X 2y 3 And The Parabola X 2 40y Where X And Y Are Measured In Mm See Fig A



Centroids And Centers Of Gravity Ppt Video Online Download




Find The Centroid Of The Area Bounded By The Parabola Chegg Com
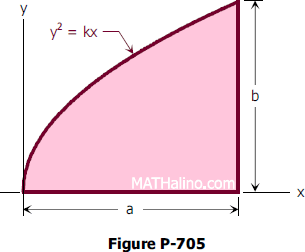



705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino



Pdf Statics Bedford Chap Daniela Ubaque Garcia Academia Edu



Lpuguidecom Files Wordpress Com 16 10 Chapter 05 Pdf



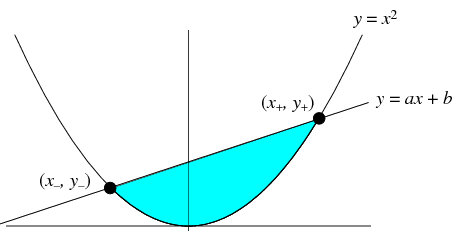
New Version Available Find The Centroid Of A Bounded Region Involving Two Quadratic Functions Youtube



Parabolic Segment From Wolfram Mathworld




Find The Centroid Of The Region Bounded By The Parabola Y X 2 The Line X 2 And The X Axis Study Com
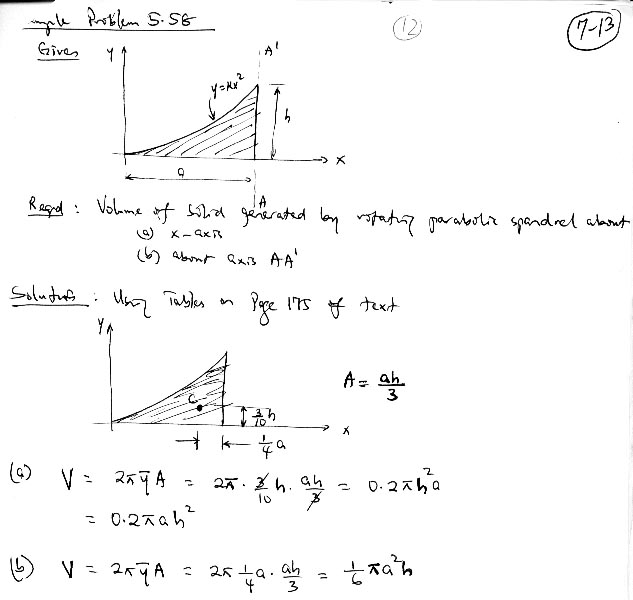



Centroids Centre Of Mass Centres Of Gravity
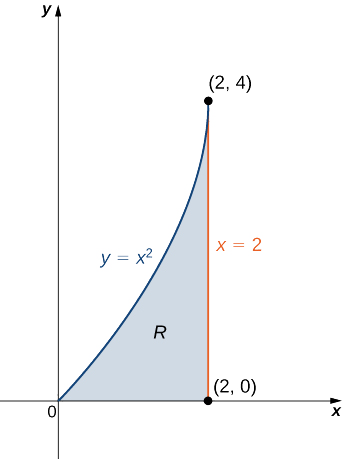



15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts




Centroid Area Moments Of Inertia Polar Moments Of Inertia Radius Of Gyration Of A Parabolic Spandrel Sub Parabolic Area




Centroids Reference Table Calcresource
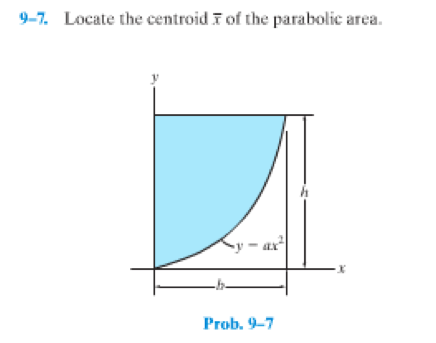



Locate The Centroid X Of The Parabolic Area Chegg Com




8 Further Applications Of Integration Further Applications Of




Solution Locate The Centroid Of The Plane Area Bounded By The Parabola The Line And The
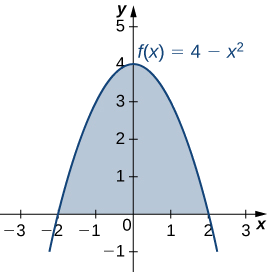



6 6 Moments And Centers Of Mass Mathematics Libretexts




Find The Centroid Of The Region Bounded By The Line Y X And The Parabola Y X 2 Study Com




List Of Centroids Wikipedia



Solved Use Integration To Compute The Coordinates Of The Centroid Of The 1 Answer Transtutors



Solved Find The Centroid Of The Area Bounded By The Parabolas X2 Y And Y 9 Course Hero




B Determine The Exact Location Of The Centroid Of Chegg Com



Http Faculty Mercer Edu Jenkins He Documents Centroids Pdf



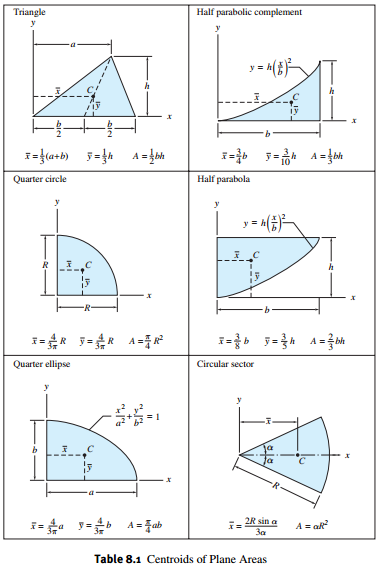
708 Centroid And Area Of Spandrel By Integration Engineering Mechanics Review At Mathalino



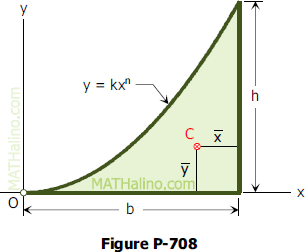
Lesson 12 Centroid Of An Area
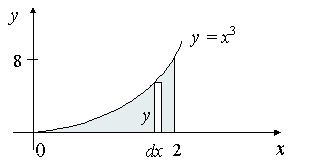



5 Centroid Of An Area By Integration



Anvari Net Dynamics Chapter 9 Pdf




Thomas Calculus 11e 1263 1564 Pages 51 100 Flip Pdf Download Fliphtml5



0 件のコメント:
コメントを投稿