I assume you want to rationalize the denominator You start with (1√2)/ (2√3) just multiply top and bottom by the conjugate of 2√3, which is 2√3 Now you have (1√2) (2√3) / (2√3) (2√3) = (1*2 2√2 1*√3 √6)/ (2^2 √3^2) = (2 2√2 √3 √6)/ (43) = 2 2√2 √3 √6 What you rationalize is the denominator of the fraction Eg 1/√2 is multiplied and divided by √2 to give √2/2 which is still irrational So you might be wondering what's the purpose of rationalising Let's do this, what is the value obtained if we add √2 √3 to 1/(√3 √2) It might be hard to tell right nowRD Sharma Solutions for Class 9 Maths Chapter 3 – Free PDF Download In Class 9, Rationalisation is one of the most important chapters RD Sharma Solutions for Class 9 Chapter 3 is about different algebraic identities and rationalisation of the denominatorA rationalisation is a process by which radicals in the denominator of a fraction are eliminated

Example Rationalise The Denominator Of 1 7 3 Root 2
Rationalize the denominator 2+root 3/2-root 3
Rationalize the denominator 2+root 3/2-root 3-SECTION 13 rAdicAls ANd rAtioNAl exPoNeNts 33 b 4√ —81a4b ∙ 2a Factor perfect square from radicand √ —81a4b4 ∙ √ —2a Write radical expression as product of radical expressions 9a2b2 √ —2a Simplify Try It #2 Simplify √ —50x2y3z How To Given the product of multiple radical expressions, use the product rule to combine them into one radical expression Given, 1/(2 √3) 2/(√5 √3) 1/(2 √5) After rationalizing each term, we get = {1*(2 √3)}/{(2 √3)*(2 √3)} {2*(√5 √3)}/{(√5




How To Rationalize The Denominator 14 Steps With Pictures
Example 3 – Simplify a) 3√40 √ b) 2√3−54 c) What if there are variables in the expression?So √7 = a/b > (1) Square on both sides, we will have 7=a^2/b^2 => 7*b^2=a^2 > (2) From this we can conclude that a^2 is divisible by 7 and thus a is also divisible by 7 So we can write a as a product of 7 and another natural number, say c => a =7* c Substitute the value of a in equation 2If √2=1414√3=1732√5=2236 and √6=2449 find the value of If √2= 1414,√3 =1732,√5=2236 and √6= 2449, find the value of 2√3 2−√3 2−√3 2√3 √3−1 √31 A
Lesson Plan in Mathematics 9 Prepared by Jessica B Alidon and Neliza A Sevilla I LEARNING OBJECTIVES After a series of illustrative examples, the Grade 9 students shall be able to 1 differentiate like radicals from unlike radicals 2 perform operations on radicals a add and subtract radical expressions b multiply and divide radical expressions 3 think and solve on problemsRationalise the denominator in each of the following and hence evaluate by taking √2 = 1414, √3 = 1732 and √5 = 2236 up to three places of decimal asked in Class IX Maths by navnit40 ( 4,938 points) rationalize the denominator by multiplying both the numerator and denominator by (2 √3) (1 x (2 √3))/((2 √3) x (2 √3)) = (2 √3)/(4 2√3 2√3
Start studying LT 56 Binomial Radical Expressions Extra Spiral Review Learn vocabulary, terms, and more with flashcards, games, and other study toolsQuestions Show answers Q Rationalize the denominator Q The number below the radical Q The process of removing a radical from the denominator QTo rationalize, the given expression is multiplied and divided by its conjugate The online tool used to divide the given radical expressions is called dividing radical expressions calculator Example 1 Divide and simplify the given radical expression 4/ (2 √3) The given expression has a radical expression in the denominator




How To Rationalize The Denominator 14 Steps With Pictures



Rationalize The Following पर म यकरण क ज य 1 3 2 3 2 3 2 2 3 6 Snapsolve
Write the rationalisation factor of 2 Answer Rationalizing factor of √5 – 2 = 11 Question If x = 3 2 , then find the value of Answer Given x = 3 2√2 (√3)2 2×2×√3 = (2√3)2 = (2√3) (2√3) 21 Question is equal to A 3 2 B C 32 D Answer 1/ √9√8 = 1/(√9 √8) × (√9 √8) / (√9√8) = √9RATIONALIZING THE DENOMINATOR A surd such as √3, cannot be simplified, Eg 2 = 2 x √3 = 2√3 = 2√3 = 2√3 This process removes the irrational number (√3) √3 √3 √3 √(3 x 3) √9 3 from the denominator and this is called rationalizing theTweet Answer this question Do you know the correct answer?




How Do You Simplify Sqrt 15xy 3sqrt 10xy 3 Socratic




Ex 1 5 5 Rationalize Denominators Of I 1 Root 7 Ii 1 Root6
Click here👆to get an answer to your question ️ If x and y are rational numbers such that 2 √(3)2 √(3) = x y√(3) , find the value of x and yMake money answering questions!Click here👆to get an answer to your question ️ Solve 2 √(3)2 √(3) 2 √(3)2 √(3) √(3) 1√(3) 1




Intro To Rationalizing The Denominator Algebra Video Khan Academy




Rationalize The Denominator 6 3 2 2 3 Brainly In
B 2 C D Answer Simplest rationalizing factor of 2√5 √3 = 1/(2√5 √3) = 2√5 √3 Question 18 If x = 2, find the value of x Answer Given, x = 2√3 = = Question 19 Write the rationalisation factor of 2 Answer Rationalizing factor of √5 – 2 = Question If x = , then (x3) 2 = A 1 B 3 C 6 D 7 AnswerWhich of the following is ( 3√2 / √7 ) in simplest form? In order to rationalize, multiply and divide the denominator of the irrational number by the rationalizing factor of the denominator and then simplify Example 1 Rationalize the denominator of √2/√7 Solution The rationalizing factor of √7 is √7 So, multiply by √7 in the numerator and denominator of √2/√7




Simplify By Rationalising The Denominator 7 Root 3 5 Root 2 Root 48 Root 18 Youtube
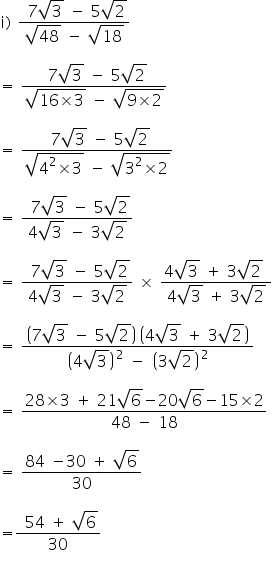



Sir Pls Solve The Following Problem Rationalize The Denominator 7 3 5 2 2 6 5 48 18 3 5 2 6 1 2 3 1 3 2 2 3 1 Mathematics Topperlearning Com Lh6vmmyy
Rationalize the denominator for each of the following expressions a 1/(2 √3) b 3/(√5 √2) c √5/(2√3 7)My book is saying that the answer is (√21)(2√2) Without a denominator Did I do something wrong or is the book wrong (it's been wrong before) Found 3 solutions by rationalize the denominator of 1/(2√3)




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium
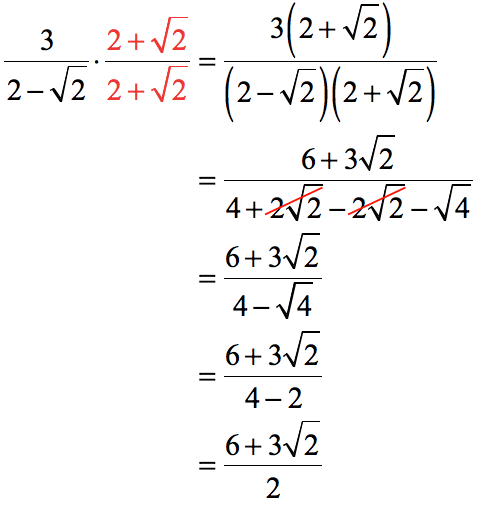



Rationalizing The Denominator Chilimath
TO PROVE 1/(2√3) is irrational We can rationalize the denominator of the above expression, & then we can proceed with our proof After rationalization 1 / (2√3) * (2√3) / (2√3) = (2Answer for question Your name Answers recent questions he ratio of boys to girls in a group is 21 If there are 22 more boys than girls, work outFind de 2 2 53 correlate the relationships solve for Find DE ??



Simplifying By Rationalising The Denominator 4 2 3 7 Studyrankersonline



How To Rationalise The Denominator 1 2 3 5 Quora
SOLUTION Sol Given x = 7 4√3 x = 7 4√3 1 / x = 1 / ( 7 4√3) rationalize denominator (7 4√3) = (7 4√3) / 49 48 = (7 4√3)2 √3 2 √3 √ 2 √ 2 x = Apr 3/19 If rationalizing the denominator, DO NOT expand the numerator If rationalizing the numerator, DO NOT expand the denominator = = = = VECTORS SUMMATIVE @ 9 IN CAFETERIA = =Roots of Positive Powers of 𝒙 – Case 1 When 𝒙≥𝟎√in 𝒙𝒏 with 𝒏 a positive integer The square roots of negative numbers are undefined in the set of real numbers




Rationalise The Denominator Of 2 3 2 3 Brainly In




Rationalize The Denominator 3 2 5 3 2 Brainly In
You can solve it by rationalising the denominator, it means to make the denominator a rational number It is as follows Multiply both the denominator and numerator by 2√3 =Let x= √2√3 Then we can write (√2√2√3)= √2x Also (√2√2√3) = √2(√2√3) = √2x So (√2√2√3) (√2√2√3)= (√2x)(√2x)Given that `x= (sqrt3 sqrt2) /(sqrt3 sqrt2)` and `y = (sqrt3 sqrt2) /(sqrt3 sqrt2)` We need to find `x^2 xy y^2` Now we will rationalize xWe know that rationalization factor for `sqrt3sqrt2` is `sqrt3sqrt2` `sqrt3sqrt2`We will multiply numerator and denominator of the given expression `x= (sqrt3 sqrt2) /(sqrt3 sqrt2)` by `sqrt3 sqrt2`, to get




How To Rationalize The Denominator 14 Steps With Pictures



Rationalise The Denominator In Each Of The Following And Hence Evaluate By Taking 2 1 414 3 1 732 And 5 2 236 Up To Three Places Of Decimal Studyrankersonline
Rationalise the denominator of 2√3 / 2√3 2 See answers khanujarashmit khanujarashmit Solution is attached below But we should multiply both numerator & denominator with 2√3 (rationalising factor) So I got the answer as 7 tapdiyaunnati tapdiyaunnati Solution is attached belowTO PROVE 1/(2√3) is irrational We can rationalize the denominator of the above expression, & then we can proceed with our proof After rationalization 1 / (2√3) * (2√3) / (2√3) = (2A easy way to understand the method to rationalize the denominator Rationalize the denominator (√2√3)/(√2√3) and ((53√14))/((72√14))




Rationalize The Denominator 3 77 V10 A 10 V Chegg Com




Example 2 Rationalize Denominators Of Fractions Simplify Ppt Video Online Download
Key Concept Case 1 If the denominator is in the form of √b (where b is a rational number), th en we have to multiply both the numerator and denominator by the same √b to rationalize the denominator Case 2 If the denominator is in the form of a ± √b or a ± c √b (where b is a rational number), th en we have to multiply both the numerator and denominator by its conjugateThe rationalizing factor of 2√3 is √3 2√3 × √3 = 2 × 3 = 6 Rationalize the Denominator Meaning Rationalizing the denominator means the process of moving a root, for instance, a cube root or a square root from the bottom of a fraction to the top of the fractionLearn special triangles radians with free interactive flashcards Choose from 500 different sets of special triangles radians flashcards on Quizlet




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Simplify Math Dfrac 4 Sqrt 3 2 Sqrt 2 Dfrac 30 4 Sqrt 3 Sqrt 18 Dfrac Sqrt 18 3 2 Sqrt 3 Math Quora
x = 7 4√3 x = 4 3 2*2*√3 x = (√4) 2 ( √3) 2 2*2* √3 x = (2) 2 (√3) 2 2*2* √3 x = (2 √3) 2 or √x = 2 √3 now putting the values2 √3 2 √3 over the denominator 2 √3 4√3 2 √3 At this point you have 2 choices You could leave this fraction as is and then cube the whole fraction Or you could "rationalize the denominator" first and then cube the resulting fraction Your choice! Express in surd form and simplify by rationalizing the denominator 3 sin 45° 2 cos 30° tan 30°




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




The Rationalisation Factor Of 2 Sqrt 3 Is 2 Sqrt 3 B Sqrt 2 3 C Sqrt 2 3 D Sqrt 3 2
Join now Rationalize the denominator 2√3/ 2√3?Rationalize the denominator 2√3/ 2√3?Here we have 2 √3 in the denominator, to rationalize the denominator we have multiply the entire fraction by its conjugate Conjugate of 2 √3 is 2 √3 Step 2 (i) By comparing the numerator (2 √3)² with the algebraic identity (ab)²=a² 2abb², we get 2² 2 (2)√3 √3² ==> (74√3)




How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation
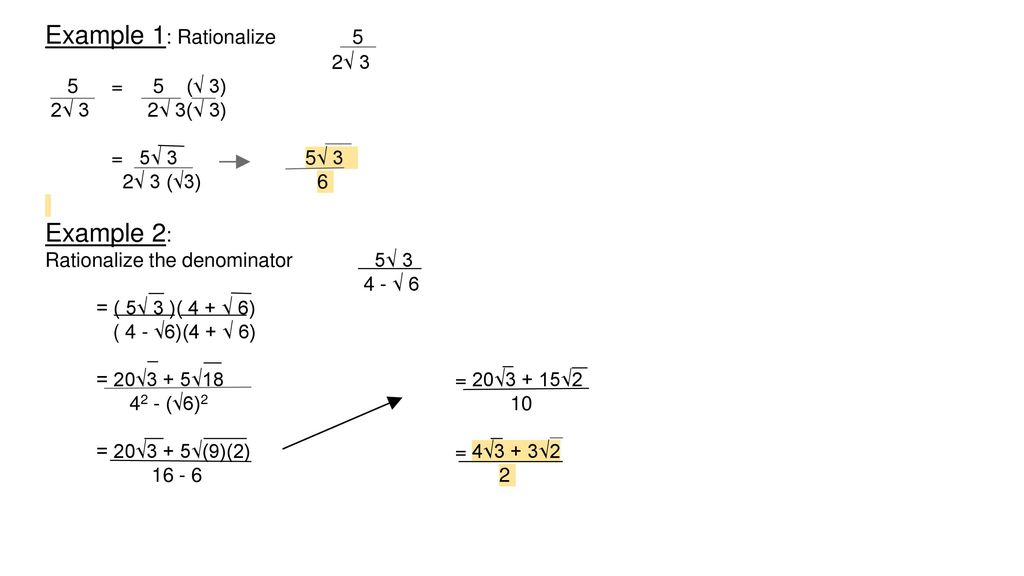
To rationalise a denominator of this type, (ignoring for a moment the 2s cancel) a) Multiply top and bottom by √3 b) then use the fact root √3 * √3=√9 = 3 so we get 2√3 / 2*3 = 2√3 / 6 Mathematics Simplify and Write in Factored Form 3(x 4) 5x Algebra Simplify Write answers in the form of a bi, where a and b are real numbersRationalizing a denominator rewriting a fraction so that the denominator contains no radicals (we'll only be working with square roots in this lesson) o a fraction such as 2 √5 can be rewritten as 2√5 5 by simply multiply the original fraction by the denominator over itself @√5 √5 A 2 √5 ∙√5 √5 =2√5 5



How To Rationalize Math Frac 1 Sqrt 7 Sqrt 3 Sqrt 2 Math Quora




Rationalize The Denominator Of 3 Root 5 Root 2
Question 1 Find the equation of the straight lines passing through the origin and making an angle of 45° with the straight line √3xy = 11 Solution As line 1 passes through origin, there won't be any intercept, and it will be in the form of y = mx (m as slope) For line 2 √3xy = 11, slope is M = √3 Here, it is given that theseSection 62 & 63 Multiply, Divide, Rationalize Radicals DRAFT 10th 12th grade 2 times Mathematics 62% average accuracy 3 years ago mpower 0 Save Edit Edit Section 62 & 63 Multiply, Divide, RationalizeIn other words, we can say, rationalizing the denominator means moving the radical term (square root or cube root) to the numerator, such that a denominator is a whole number When we rationalise the denominator, then it becomes easy to find the sum or difference of given fractions (12√3)/(2√3) = ab√3 and find the value of a and b



Rationalize The Denominator I 1 5 Ii 2 3 7 Iii 1 3 2 Iv 1 3 5 2 2 V 12 4 3 2 Sarthaks Econnect Largest Online Education Community




After Rationalizing The Denominator Of 5 2 3 7 4 3 And Simplifying We Get 11 M 3 Then The Value Of M Is
Correlate the relationships Solve for x Side relationship of a 30 ° − 60° − 90° right triangle Substitute Simplify Side relationship of a 30 ° − 60° − 90°= 2 ∙ (5√3 ) ??




After Rationalizing The Denominator Of 3 12 2 3 And Simplifying We Get 2 6 3 2 M 3 5 Then The Value Of M Is




Rd Sharma Class 9 Maths Solutions Chapter 3 Rationalisation



1




Rationalize The Denominator Expii




Rationalise The Denominators 1 3 Root 2 2 1 Root 6 Root 5 3 16 Root 41 5 Youtube




The Simplest Rationalisation Factor Of 2sqrt 2 Sqrt 3




Rationalise The Denominator Of 2 Sqrt 3 Sqrt 5 Youtube




2 Is Divided By 3 Root 3 By Rationalizing The Denominator Brainly In




After Rationalizing The Denominator Of 7 3sqrt 3 2sqrt 2 We Get The Denominator As




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is



After Rationalising The Denominator Of 7 3 3 2 2 We Get The Denominator As A 13 B 19 C 5 D 35 Sarthaks Econnect Largest Online Education Community




Simplify By Rationalising The Denominator 2 6 5 3 5 2 6



Q Tbn And9gcsb2rnpibjsemfefshm1leviszzhattq67fri0obpzhq J Lxfh Usqp Cau
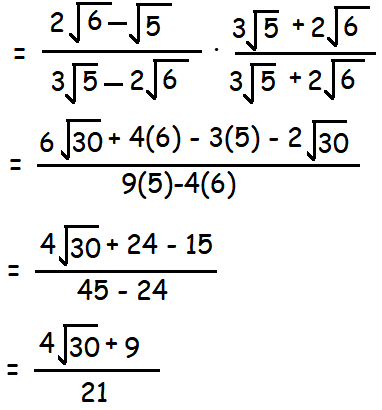



Practice Problems On Rationalizing Denominator




How To Rationalize Math Frac 1 Sqrt 2 Sqrt 3 Sqrt 5 Math Quora
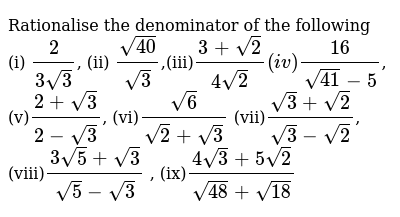



Rationalise The Denominator Of The Following I 2 3sqrt3 I
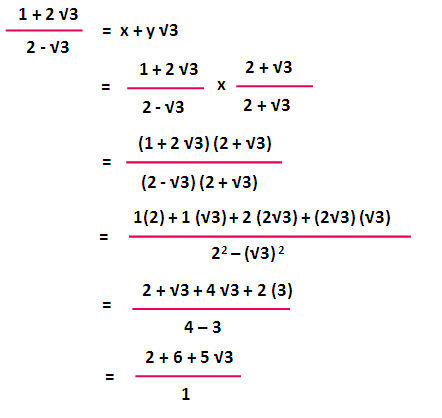



Rationalizing The Denominator With Variables




Rationalize The Denominator 12 5 3 And Hence Find The Value Of A B In 12 5 3 A 5 B 3




3 2 1 2 5 3 Rationalise This Term In Briefly Brainly In



After Rationalising The Denominator Of 7 3 3 2 2 We Get The Denominator As A 13 B 19 C 5 D 35 Sarthaks Econnect Largest Online Education Community




Multiply In The Numerato I 2 136 Simplify By Rationalizing The Denominator 2 3gi



Rationalization Of Surds Assignment Point




Multiplying And Dividing Radical Expressions




Rationalize The Denominator And Simplify Polynomials Maths Class 9




Rationalize The Denominator Of 3 Minus Root 2 By 3 Root 2 Brainly In




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




Rationalise The Denominator Of 1 8 5 2 Rationalise The Denominat




Rationalization To Find Limits L V17 Clh S1




Example 19 Rationalize The Denominator Of 5 3 5 Examples



Simplifying By Rationalising The Denominator 1 3 2 5 Studyrankersonline




Rationalize The Denominator 2 3 5 Brainly In



Kqwakixxppybrm




R D Sharma Solutions Class 9th Ch 3 Rationalisation Exercise 3 2




Rationalise The Denominator Of 1 2 Sqrt 3 Youtube




Example Rationalise The Denominator Of 1 7 3 Root 2




Rationalise The Denominator And Simplify 1 2 3 2 2 Brainly In



1



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Chapter 3 Rationalisation Fraction Mathematics Rational Number




Rationalise The Denominator 4 3 5 4 3 5 Youtube




Rationalize 2 3 5 2 2 3 3 Brainly In



Rationalize The Denominator I 1 5 Ii 2 3 7 Iii 1 3 2 Iv 1 3 5 2 2 V 12 4 3 2 Sarthaks Econnect Largest Online Education Community




Example 2 Rationalize Denominators Of Fractions Simplify Ppt Download



Chapter 5 Radical Expressions And Equations Ppt Download



Q Tbn And9gcrdpezo9dtgnwo1evsbut2dx1dc1fff 52tf0 Uifj9lvz9 Uby Usqp Cau



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Rationalise The Denominator Of 1 Root3 Root2 Brainly In




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation




Rationalize 1 7 3 2 Maths Questions




R D Sharma Solutions Class 9th Ch 3 Rationalisation Exercise 3 2




Rationalizing The Denominator 2 3 5 By 2 2 3 3




Rationalize The Denominator Squareroot 1 2 Chegg Com




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation
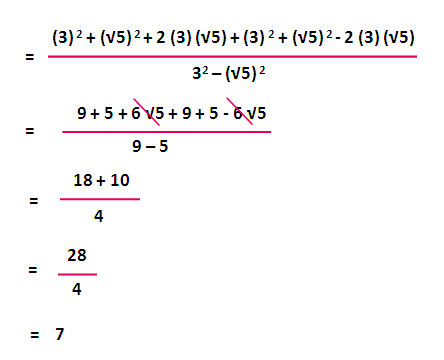



Rationalizing The Denominator With Variables




Rationalize The Denominator And Simplify 5 2 3 7 4 3 Brainly In




Rationalize The Denominator Meaning Methods Examples




Rationalize The Denominator Of 5 3 Root 2
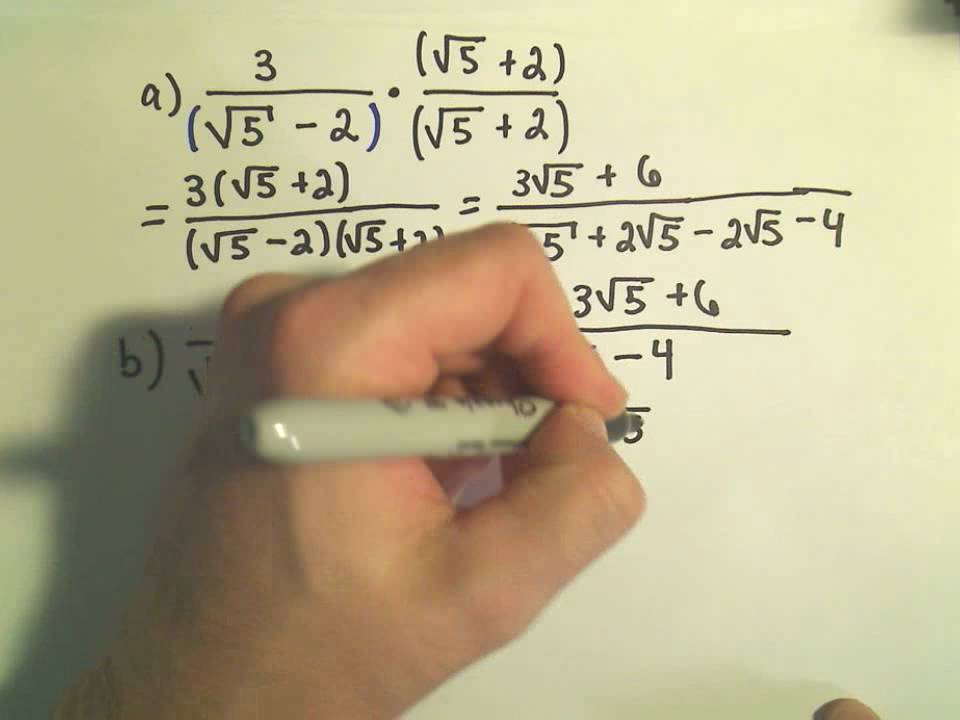



Rationalizing The Denominator Example 1 Youtube



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




How To Rationalize The Denominator 14 Steps With Pictures




Rationalise The Denominator 2 3 2 Brainly In




Example Rationalise The Denominator Of 1 7 3 Root 2



How To Rationalize The Denominator Of 1 2 1 3 2 1 3 Quora



Rationalise The Denominator Of 1 3 2 And Hence Evaluate By Taking 2 1 414 And 3 1 732 Up To Three Places Of Decimal Studyrankersonline
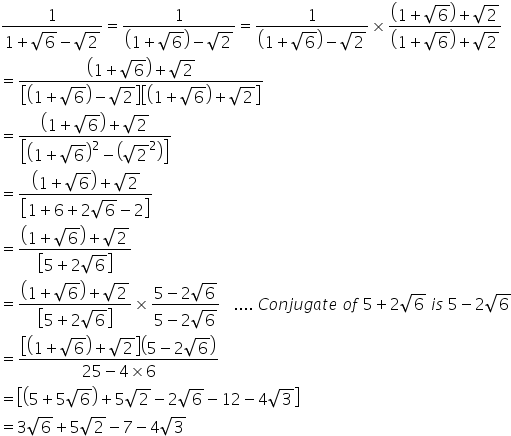



Rationalise The Denominator Of The Expression Mathematics Topperlearning Com Hvx3khh



Simplifying By Rationalising The Denominator 3 5 3 2 5 3 Studyrankersonline




Example 18 Rationalize The Denominator Of 1 2 Root 3
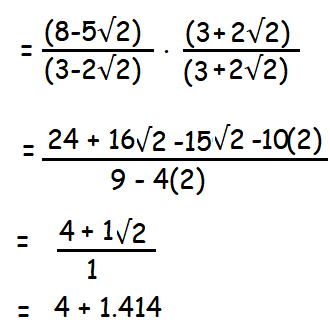



Practice Problems On Rationalizing Denominator



Write Lowest Rationalising Factor Of 15 3 2 Mathematics Topperlearning Com Mhligm11




Rd Sharma Class 9th Solutions Chapter 3 Rationalisation




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Exercise 3 2




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download




7 5 Root 3 5 Root 2 Rationalise The Denominator Youtube




Solved Rationalize The Denominator And Simplify The Follo Chegg Com




Write The Rationalizing Factor Of The Denominator In 1 2 3



0 件のコメント:
コメントを投稿