ピタゴラス の 定理 問題 257777-ピタゴラスの定理 問題

Oct 13, 08 · この問題を解くには、学生時代からの時間（約35年間）が経ちすぎていて、3つのツール（ピタゴラスの定理、三角関数、ルート計算方法）をすっかり忘れていたのです。 なので、この問題を解く前に、この3つのツールを復習します。Jan 10, 18 · 三平方の定理を利用して四角すい、円すいの体積を求める問題です。 まずは基本的な円錐、正四角錐の体積の求め方をしっかり確認してから、いろいろな応用問題を解くようにしてください。 円錐の体積 下のような底面積の半径が6cm、 17年2月14日「ピタゴラスの定理（三平方の定理）」の証明です。ピタゴラス自身がおこなったとされる方法をアニメ化しています。PYTHAGOREAN THEOREM Proof by

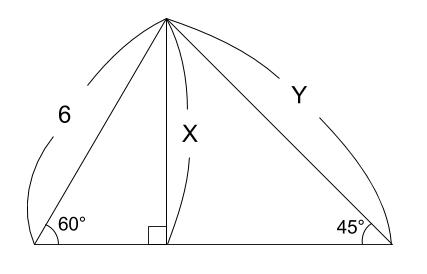
中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

ピタゴラスの定理 問題

ピタゴラスの定理 問題-Mar 07,  · 今回の ピタゴラスの定理 は、 ピタゴラス 数を求める アルゴリズム の問題です。Feb 18, 17 · ピタゴラス数とは 三平方の定理（ピタゴラスの定理）にでてくるあの式です。自然数の組の場合、ピタゴラス数と呼ばれます。 三平方の定理(ピタゴラスの定理)とは、「直角三角形の3辺の長さをそれぞれa,b,c(斜辺)としたとき、\(a^2b^2=c^2\)の関係がある。

数学 中3 61 三平方の定理 基本編 Youtube

対象商品 ピタゴラス®問題集 ￥1,000 残り2点 ご注文はお早めに この商品は、岩手なかちゃんショップが販売し、Amazon Fulfillment が発送します。 ピープル 3・4年生の小学生ピタゴラス PGS111 ￥2,536 この商品は、Amazoncojpが販売および発送します。 通常配送初等幾何学 における ピタゴラスの定理 （ピタゴラスのていり、 英 Pythagorean theorem ）は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は が成り立つという 等式 の形で述べられる 。三平方の定理(別名ピタゴラスの定理)とは、底辺が $a$、高さが $b$、斜辺が $c$ である直角三角形において、$$a^2b^2=c^2$$ が成り立つことでしたね。 この式を証明するポイントを一言で言えば

Jan 23, 14 · 三平方の定理(ピタゴラスの定理)を面積図を使って証明します。小学生向けの問題も掲載。そして、中学受験によく出る 直角三角形の長さの比も紹介しますね。定義《ピタゴラスの33 3 つ組》 c c が整数であるような直角三角形を ピタゴラスの三角形 (Pythagorean triangle)と呼ぶ また, ピタゴラスの三角形の 3 3 つ組 (Pythagorean triple)と呼ぶ 三平方の定理により, これは方程式 (a,b,c) (a,b,c) に他ならない c c が互いに素で直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 （三平方の定理）と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス (cBC570cBC500)が発見したかどうか確証があるわけではありません。 ピタゴラスの定理 3世紀にディオゲネス・ラエルティオスは『哲学者列伝』の中で「算数家のアポロドロスによれば

May 05, 19 · a 2 b 2 = c 2 ⇒ ( a t) 2 ( b t) 2 = ( c t) 2 つまり，ピタゴラス数がひとつみつかったら，その自然数倍は必ずピタゴラス数です． a, b, c a, b, c が互いに素であるようなピタゴラス数は 原始ピタゴラス数 と呼びます．たとえば， (3, 4, 5), (8, 15, 17) ( 3, 4, 5), ( 8, 15, 17) などは原始ピタゴラス数です．また， (9, 12, 15), (10, 24, 26) ( 9, 12, 15), ( 10, 24, 26) などはピタゴラス数Mar 22, 17 · 三平方の定理は、ピタゴラスの定理とも言われ、直角三角形の3辺の長さの関係を表す等式のことをいいます。 この定理を使えば、直角三角形の2辺の長さがわかっていれば、残りの1辺の長さもわかってしまうのです。Oct 27,  · 逆ピタゴラスの定理(符号問題)⚠️ 3 ツイート宇宙の星屑板 2121 「逆ピタゴラスの定理(符号問題)⚠️」 👽：(2/3)(1/3)=3/3 01×03×(10)=30

中３数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Mar 15, 01 · ピタゴラスの定理 大矢真一著 参考 上の問題とと同様にP，Q，R，Sを作る。そして、ABに平行でCを通るIM，KN，LFを作る。図1のように1から8を定める。 四辺形KNAJは、平行四辺形でピタゴラス数と三角形 ピタゴラス数はa2 b2 = c2 の関係式があります． ピタゴラスの定理より，3つの辺の長さがa, b, c である 三角形は直角三角形になります． 6 8 10 9 12 15 5 12 13 3 4 5 一番長い辺（長さc の辺）が斜辺になります． 体験授業（数学） / 78面積(高校数学 ii) 面積(高校数学 iii) や行 ユークリッドの互除法(高校数学 a) 余弦定理・正弦定理(高校数学 i) ら行 立方体倍積問題;

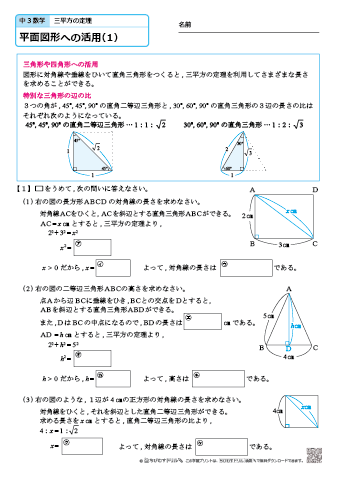
中学３年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生

Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ

Aug 08,  · 今日の問題です。記事の末尾にちょっとしたお知らせを載せていますので、それも見て下さいね♪↑の図のように、一辺2cmの正方形とおうぎ形が重なったような形を考えて、正方形の一辺の長さだけから、おうぎ形の面積を求めようというものです。動画はこちら。Ama02 練習問題へ u adc は直角三角形であるから，ac の長さがわかればad の長さが求められる。 そこで，ま ず，u abc に注目し，三平方の定理を利用して，ac の長さを求める。 u abc で三平方の定理より ac 5 5 10 5 cm＝－＝（）_i2 2 ←ac ab bc＝－22 さらに，u adc で三平方の定理よりおなじみの問題。 全て円弧です。 A 約31．5c㎡ 100π／3 正方形が三つ並んでいます。 実は、ピタゴラスの定理を使わなくても簡単に求められます。 A 45° 簡単にできると思って取り組んだら、けっこう難しかった問題。

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生

直角二等辺三角形befの面積は？（06年算数オリンピック、ファイナル問題より）() 色のついた部分の面積合計は？（大阪星光学院中学 12年）() 三平方の定理、小学生バージョンの解き方（江戸川女子中 09年）()ここではこのピタゴラスの定理が人間の知恵の象徴として使われています。 問題1 上の2つの正方形を図のように分割します。 これを並び替えると、下の大きな正方形を作ることができます。 このことでピタゴラスの定理を証明してください。Jun 01, 17 · 下のタイルの模様から，ピタゴラスの定理が見えるでしょうか。 図形を調べるときは，どんな見方をするとよいのでしょうか。 ピタゴラスは，寺院を訪れたとき，床のタイルの模様からピタゴラスの定理を発見したと言われています。 図形

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

連立漸化式(高校数学 b) 連続関数(高校数学 ii)6．実際の問題への応用 その1 （1） ピタゴラスの定理より AC＝10cm 対角線3等分の定理より AR= cm 2 対角線3等分の定理より 2 （3） 五角形PBQSR＝長方形－ APD－ DQC－ DRS ＝48－12－12－8＝16cm 2 ※この定理を知らなければ・・・・ちょっと大変かも。(@_@) その2世界を変えたピタゴラスの定理 学んだまとめ 今回のschooの講義は！ おとな数学塾〜中学数学を楽しく学びなおす〜 世界を変えたピタゴラスの定理 21年6月24日 木曜日 00 2100 中島 隆夫先生 江戸時代の人は数学を楽しんでいた 江戸時代、数学は娯楽」だった 江戸時代には「農業、商業

しょうちゃん 公式ブログ 算数の問題を解いてみる その84 ピタゴラスの定理 円の性質 Powered By Line

高校入試レベル 三平方の定理 使います Youtube

・逆ピタゴラスの定理 S．H 氏 直角三角形とくれば三平方の定理（ピタゴラスの定理）がすぐ思い浮かぶと思うが、最近 逆ピタゴラスの定理なるものがあることを知った。 逆ピタゴラスの定理 直角を挟む2辺の長さを a、b とし、直角の頂点から斜辺に下ろした垂線の長さを h とすAug 05, 19 · 三平方の定理（ピタゴラスの定理）の例題や計算のやり方、証明、応用・難問などのまとめはこちらです 「三平方（さんへいほう）の定理」は、 中学数学で最後に出てくるけど、1番大事な定理の1つです。 高校入試では、複雑な図形の問題が出題されますが、 直角を探したり、 補助線をうまく引くことで直角を作ったりして、 三平方の定理を使える形にするFeb 15, 19 · 三平方の定理は別名ピタゴラスの定理と言い、それを満たす整数をピタゴラス数と言います。 その三つの数を ( a, b ,c )とします。自然数m , n を用意すると、 ( a, b ,c )は次のようにあらわすことができます。 a＝m^2n^2 , b=2mn , c=m^2n^2 この式はピタゴラス数の

三平方の定理の練習問題10問 解き方の解説 数学fun

三平方の定理 無料で使える中学学習プリント

三平方の定理（ピタゴラスの定理）と三平方の定理の逆、直角三角形の確かめを練習します。 プリント5枚 中学3年生 数学 三平方の定理・平面図形への活用 練習問題プリントJun 22, 18 · 古代ギリシャの数学者ピタゴラスが生まれる2千年も前から、人類はすでに「ピタゴラスの定理」を理解して建築設計に利用していた可能性が濃厚になってきた。その動かぬ証拠がストーンヘンジだ。 古代遺跡研究家のロビン・ヒース氏によると、ストーンヘンジ三平方の定理（ピタゴラスの定理）： ∠ C = 9 0 ∘ \angle C=90^{\circ} ∠ C = 9 0 ∘ であるような直角三角形において， a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2

中学3年の数学 動画 三平方の定理 基本編の問題 19ch

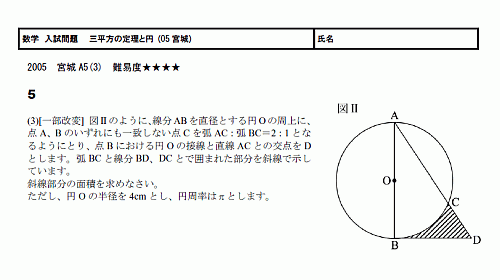
三平方の定理と円 スタディーx

三平方の定理（ピタゴラスの定理）の応用問題パターン10選 三平方の定理（ピタゴラスの定理）は、直角三角形において成り立つ定理です。 また、どんな定理だったかと言うと、$3$ 辺の長さについての定理Mar 06, 21 · ピタゴラス数とは，直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理（三平方の定理）を使うと， a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) (a,b,c) (a, b, c) をピタゴラス数と呼ぶ。 と言うこともできます。 例えば，Aug 14, 18 · ピタゴラスの定理ってご存知ですか？中学3年生で『三平方の定理』として勉強しているはずです。しかしその証明ってできますか？小学生でも分かるようにピタゴラスの定理を証明する方法を紹介します。ぜひお子さんとやってみて下さい。

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

三平方の定理の証明と使い方

May 19,  · 逆ピタゴラスの定理を使えば， 命題1 を図形的に示すことができます。 まず，斜辺を ，残りの2辺を ， となる直角三角形を用意します（ ， ， はピタゴラス数）。このとき，斜辺からの三角形の高さを とすると，逆ピタゴラスの定理より ，すなわち となります。Oct 04, 06 · ピタゴラスの定理がわかれば，球面幾何学の意味がすっきりし，双曲幾何学が手に取るようにわかります。さらに ピタゴラスの定理見方を変えて再度吟味してみると，球面幾何学の意味がすっきりし，双曲幾何学が手に取るようにわかります。さらに永久問題の平行線の公理を美しく解Jan 15, 17 · として、z,xおよびyの間にピタゴラスの定理を適用してみると、『虚数の2乗は－1』の大原則から、 e^iφ^=√(x^2^y^2^)=√(cos^2^φsin^2^φ) となる筈だが、虚数の原則は無視する不思議な数学的論理即ち、

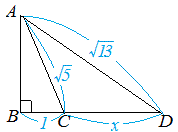
三平方の定理の応用

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

Nov 28, 16 · DFの長さをxcmとして、三平方の定理（ピタゴラスの定理）に代入してみると、 13² = 5² x² x = 12 あら不思議！ 長さがわからない直角三角形の辺を求めることができたね。 ＞＞三平方の定理（ピタゴラスの定理）の計算問題にチャレンジ！様々な角度から"ピタゴラスの定理にまつわる話題"を明解かつコンパクトに紹介したのが本書です。 内容（「MARC」データベースより） ピタゴラスの定理は、おそらく最も有名な定理ではないか。 この定理を使い、学生時代に問題を説いた経験がある人A b c a b c は直角三角形なので、三平方の定理（ピタゴラスの定理）より、 l 2 = 2 2 三平方の定理 発展問題まとめ お疲れ様でした!入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

無料ダウンロード三角形 の 法則 最高のぬりえ

Feb 13,  · 三平方の定理は別名ピタゴラスの定理とも呼ばれ， a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) はピタゴラス数と呼ばれます。中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 答えと解答はこちら。 高校入試 では 三平方の定理 を使った問題は必ず出ます。 （出ると思います。 ） 定期テストで平均点レベル、あるいは平均点以下の中学生は、この問題を確実に正解できるようにしてください。 （1）まず、その問題が、どの項目からの出題か考える。 見たことのない文章問題で年度 千葉県公立高校入試問題・前期数学 第三問 (二次関数・ピタゴラスの定理・線分比) 解説 投稿日：年4月24日 更新日：年5月12日

三平方の定理について考える１ 教科書 大日本図書 の証明方法 身勝手な主張

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

三平方の定理の練習問題10問・解き方の解説 管理人 5月 27, 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっているので、ひとつずつポイントを抑えて問題に慣れて

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

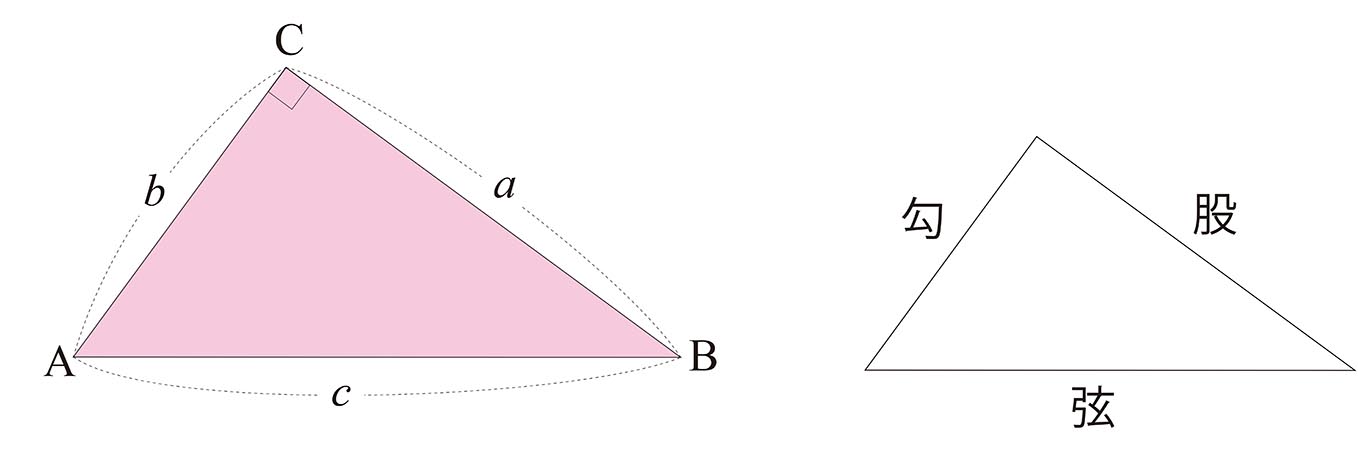
コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

投稿１０３６

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

Mathematics 三平方の定理 ３ いろいろな三角形 働きアリ

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理の証明と使い方

コラム ピタゴラスの定理 江戸の数学

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

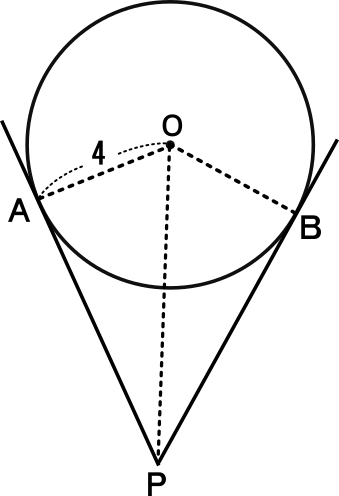
中学３年数学練習問題 三平方の定理の復習テスト

三平方の定理

1

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理の証明と使い方

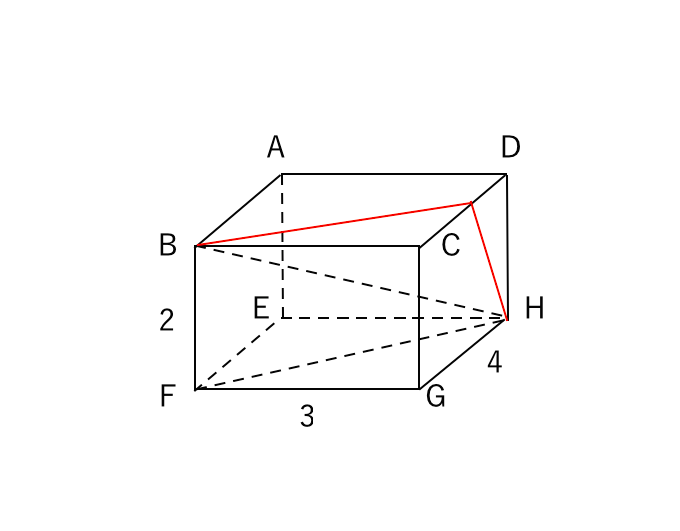
三平方の定理 立体 苦手な数学を簡単に

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4

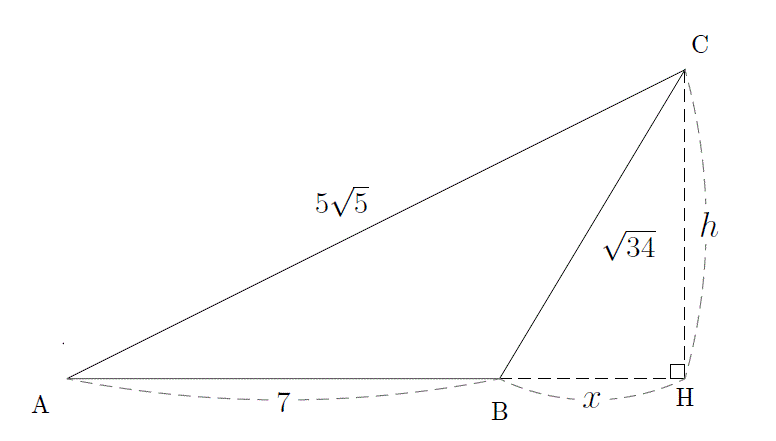
かみのドリル 三平方の定理

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

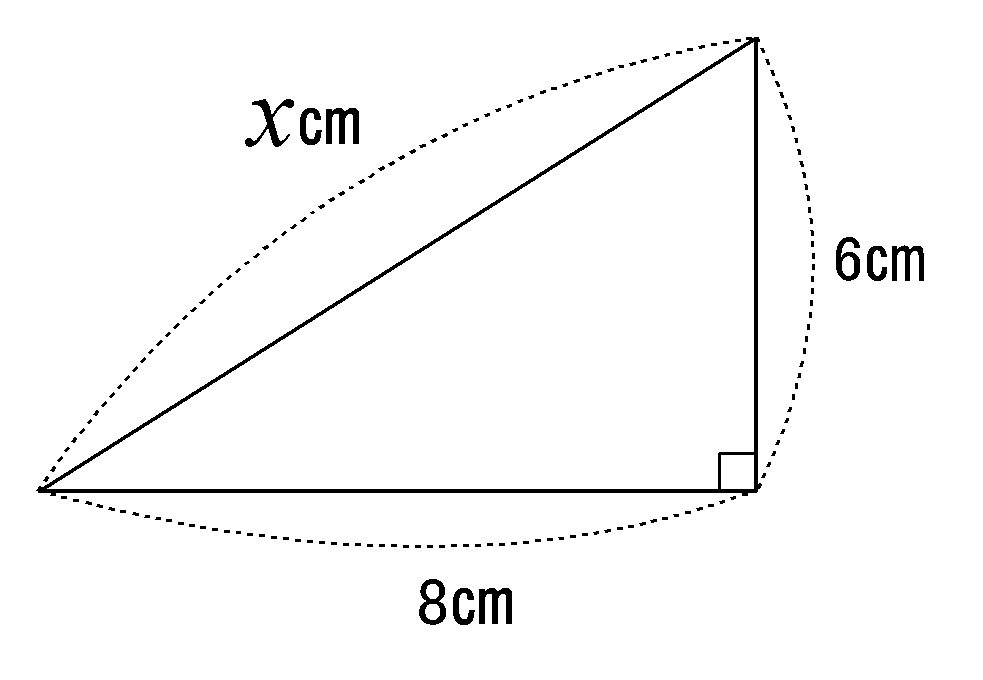
Wordで使える 三平方の定理の図 Wordで数学問題プリントを作ろう

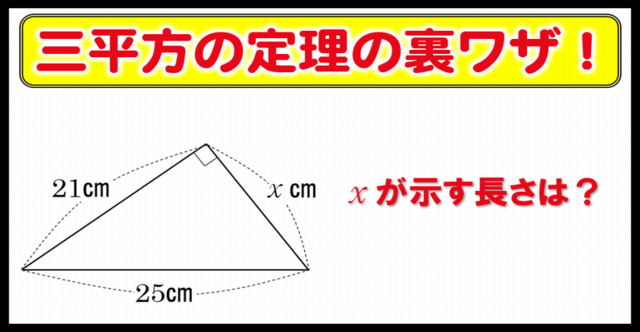
5秒以内に解けますか 賢く解きたい三平方の定理の裏ワザ 暇つぶしに動画で脳トレ

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

ピタゴラスの定理 Wikipedia

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

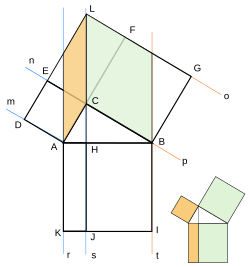
ピタゴラスの定理 Wikipedia

中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 受験と家庭教師 掲示板 s 楽天ブログ

1

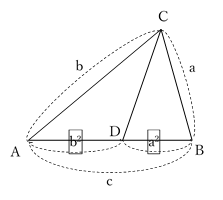
三平方の定理 おやじさん ネット

1

中学受験算数 等積変形の利用 ヒポクラテスの月

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

Use Of The Pythagorean Theorem V2 三平方の定理 Geogebra

ロイヤリティフリー三 平方 の 定理 小学生 子供向けぬりえ

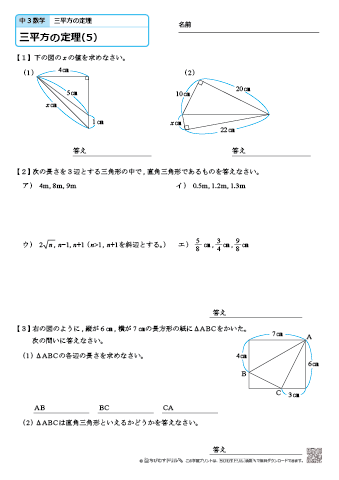
中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

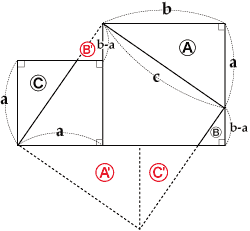
コラム ピタゴラスの定理 江戸の数学

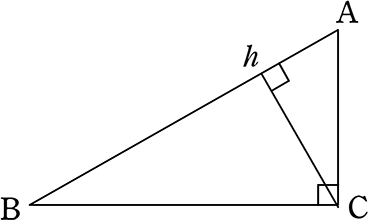
中学数学 三平方の定理

数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

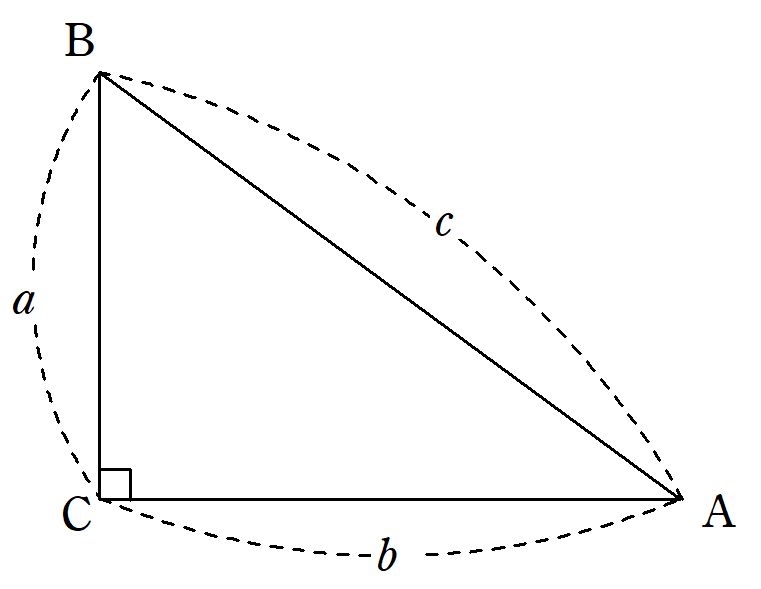
三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

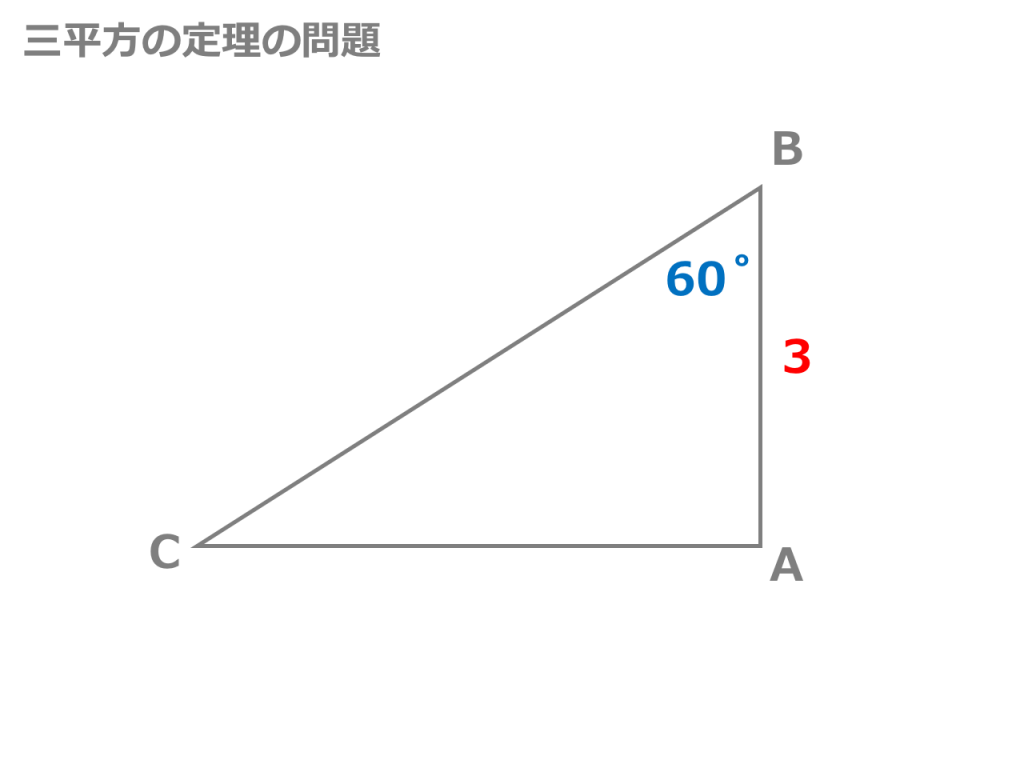
3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

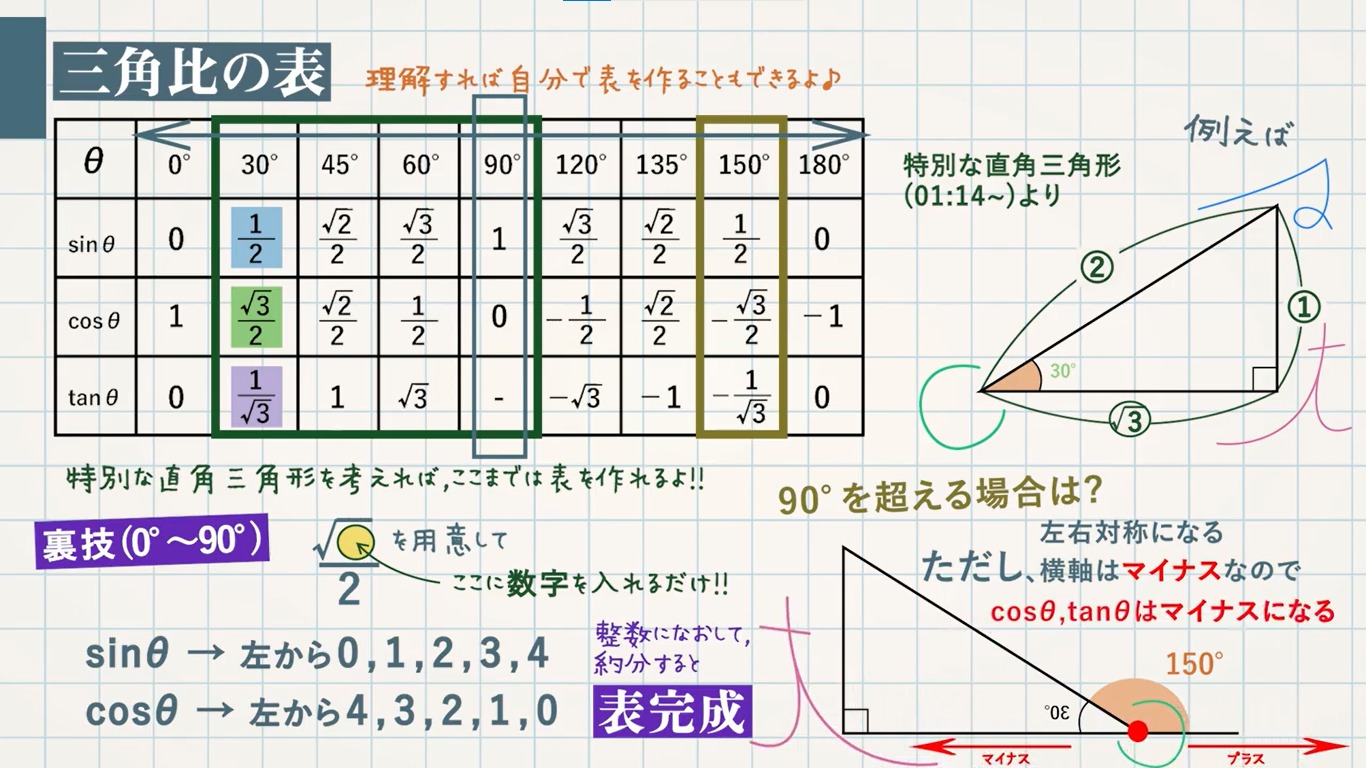
三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

世界が変わる裏技 三平方の定理を５秒で計算するテクニック Youtube

Studydoctor三平方の定理と四角形への利用 中学３年数学 Studydoctor

三平方の定理 問題 Youtube

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

数学 中3 61 三平方の定理 基本編 Youtube

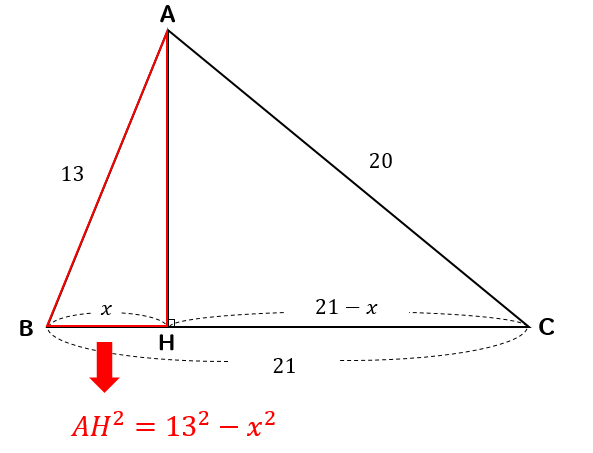
三平方の定理 方程式を利用する発展問題を解説 数スタ

数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

1

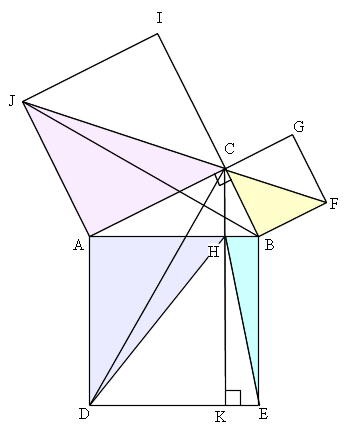
Mathematics 三平方の定理 １ 三平方の定理の証明 働きアリ

三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

三平方の定理 ピタゴラスの定理

ピタゴラスの定理 Wikipedia

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

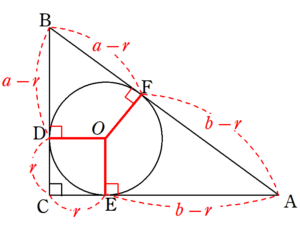
三平方の定理の証明 内接円の利用 Fukusukeの数学めも

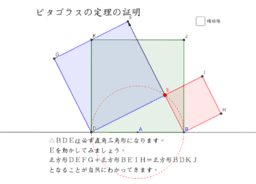
ピタゴラスの定理 三平方の定理 の証明 Geogebra

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三平方の定理の適用 ２０１７年度前期日程の奈良教育大学教育学部数学教育専修の入試問題 身勝手な主張

世界一わかりやすい数学問題集中３ ７章 三平方の定理

世界一わかりやすい数学問題集中３ ７章 三平方の定理

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

中学生 数学 3年 三平方の定理 ピタゴラスの定理 練習問題 受験と家庭教師 掲示板 s 楽天ブログ

三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear

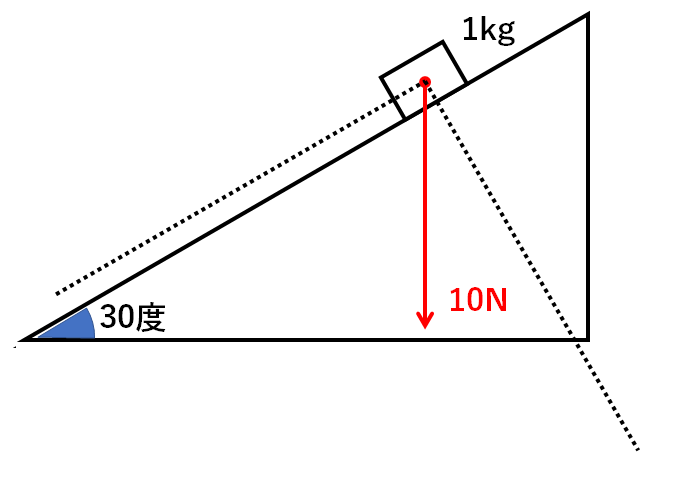
中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理

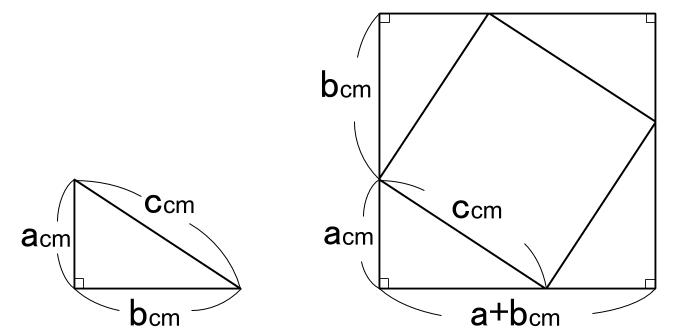
中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

Math 高校入試の難問 三平方の定理 30 60 90 1 2 3と1 2 3 30 60 90 働きアリ

三平方の定理の応用

Incoming Term: ピタゴラスの定理 問題, ピタゴラスの定理問題集,