今回は倍数の数え方についてパターン別に解説しました。 (1)で解説したように、個数の数え方には注意です。 ~40を数えるというときには、 「1~40」引く「1~19」というイメージを持っておきましょう。 「または」「~であるが~でない」など3の倍数出力プログラム このプログラムは、for 文内の処理を10 回繰り返し、そのうち i が 3 で割り切れる時のみ、出力し、合計値に加算しています。 2回目の改造 3の倍数のうち、2の倍数でない値のみ合計値として加算するように修正します。倍数算とは 倍数算とは2つの異なる数量があり、やり取りのあとの数量関係からそれぞれの数量を求める問題です。 具体的には以下のような問題。 倍数算の例題1 A君とB君の所持金の比は5:4だったが、A君がB君に400円あげたら二人の所持金の比は1:2になった。 A君の最初の所持金を求めよ。 このように2つの数量が比で与えられるだけでなく、「2倍」や「 1 4 1 4
倍数 公倍数の求め方 もう一度やり直しの算数 数学
倍数の求め方 小学生
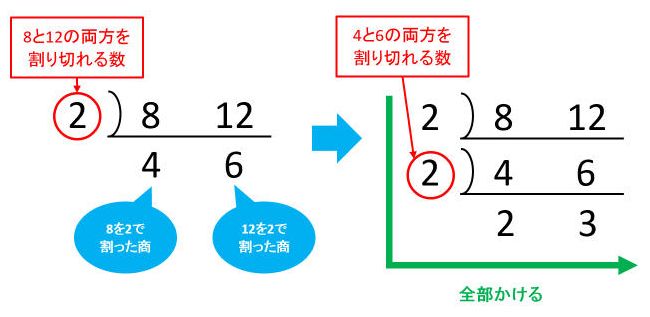
倍数の求め方 小学生- 志願倍率は「志願者数÷募集人数」で表されます。 志願倍率は、学校に願書を提出して、その大学の入試を受験する権利を得た受験生に対する倍率のことです。 例えば、願書を提出して受験したいですと言った志願者が400人いて、募集人数が0人の場合は、「400÷0=2」となって、志願倍率は「倍」ということになります。 志願倍率=志願者数÷募集人数 最小公倍数の求め方を2つ紹介します。 基本的な解き方となる「すだれ算」と、扱う数が大きいときに使う「ユークリッドの互除法」です。 最小公倍数はすだれ算で求める 最小公倍数を計算で求めるためには、最大公約数の時にも使った「すだれ算」を使います。



倍数とはどのような数ですか 用語の区別と最小公倍数の求め方に慣れよう 中学受験ナビ
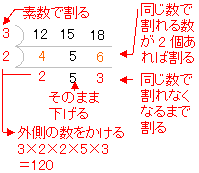
公約数・公倍数を計算していく際にも、この素因数分解は欠かせません。 たとえば、12と18の公約数や公倍数を求めたいとします。 そんなときは、まず12と18を素因数分解してみましょう。 12=2×2×3、18=2×3×3です。 公約数を探す、というのは、「12= × 、18= × としたときに、 に共通して入る数を探す」ということでもあるので、それぞれ分解して出てき約数と倍数では、両方とも 掛 か け算や割り算を利用して問題を解きます。 考え方は違いますが、似た方法によって問題を解いていくことになります。 またこのとき、約数では最大公約数という言葉があります。 倍数については、最小公倍数という言葉 psrの計算方法 psr = 時価総額 ÷ 売上高 参考(perの計算方法) per = 株価 ÷ 1株あたり純利益 詳細記事:per(株価収益率)のやさしい説明、3分でわかる投資の基礎 参考(pbrの計算方法) pbr = 株価 ÷ 1株あたり純資産 詳細記事:pbr(株価純資産倍率)のことがスッキリわかるたった1つの考え方
「濃縮倍数」を利用してブロー量を計算する方法 ブロー量とは「水の濃縮」を緩和するため、排水する水の量のことです。 濃縮倍数を決定した後、ブロー量を求める計算式は以下のようになります。 ブロー量={蒸発量÷(濃縮倍数1)}飛散量最小公倍数を求める計算機 留意事項 最小公倍数 (LCM)を簡単に求める計算プログラムです エクセルじゃないですが、最大5つの数に対して計算可能です 入力値は最大5桁までの整数に限ります(負荷の関係で適当に制限かけてます) 入力値が「0」の場合は次の問題も、上の例と同じ考え方で、求めることが出来ます。 ≪ (1)「3の倍数である整数の個数」を求める問題 ≫ ここでは、 「1から100までの整数」の中で、3の倍数の個数を考える ので、3×(整数)で表される、一番大きい(整数)を、求めてみましょう。 100÷3 を計算します。 100÷3= 33・・・1 (100 = 3×331) 商は、「33」となることから、 「33個」と分かります
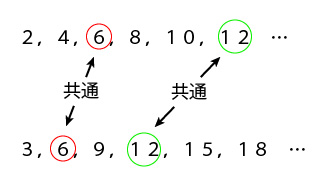
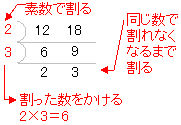
公倍数の求め方と計算 公倍数を求めるときは、それぞれの数の倍数を順番に計算して、共通の倍数を見つけましょう。下記の問題の公倍数(1~10倍まで)を求めてください。 5と10公倍数 まずは5と10の倍数を小さい順に書き出して、共通する倍数を見つけます。使い方をよく理解していないと間違った受け取り方をして状況を誤解してしまうこともある。 たかが倍率。されど倍率。 受験生として正しい倍率の意味を知り、数字に惑わされないようにしよう! 高校受験の倍率とは? あまり難しく考える必要はない。最大公約数 を求める1つの方法は,共通な数で割れるだけ割っていく方法です. このとき,共通に割れる数の積が最大公約数です. 最小公倍数 を求める方法は,これと同様ですが,割った数と残った数を掛けます. 例 次の例で, 12 , 18 の最大公約数は 6




小学生 倍数の見分け方は 三 四 六 九などの分かりやすい判定法 そうちゃ式 受験算数 新1号館




は7の倍数 7の倍数判定法 前編 Youtube
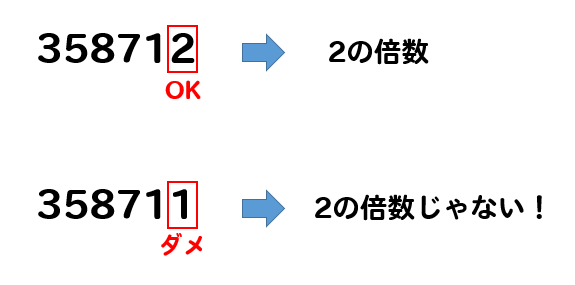
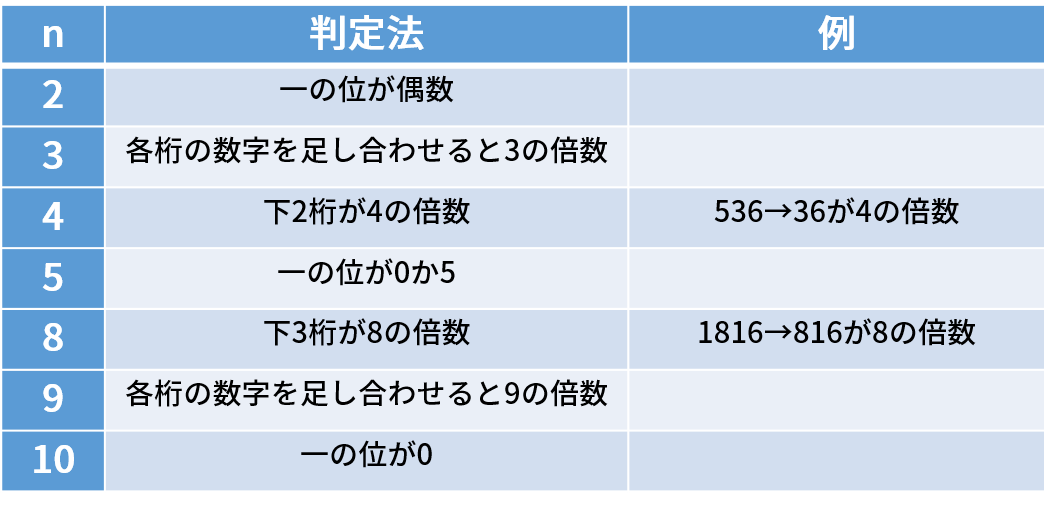
倍数についての基礎があやふやな場合は、まずは倍数の意味と求め方をご覧下さい。 倍数の意味にプラスして、公倍数・最小公倍数の意味と地道な求め方も身につけましょう。その方が 公倍数・最小公倍数に対する理解が深まります 。小野測器減衰をあらわす係数の意味と求め方 (page2) 3 減衰の効果 ここまでは、振幅が指数関数的に減衰していく状態を前提に減衰比や損失係数の求め方について説明しましたが、ここからは減衰比が実際の振動で物理的にどのような意味を持つかについて3の倍数は、末尾の文字だけで判断することはできないが、 全ての桁を足すと3の倍数になる という性質がある。 今、ある正規表現 r が、別の正規表現 s と a を使って、 r = s ra (sまたはra) と表せるとき、 r は r = sa* (sの後にaが0個以上) と求め
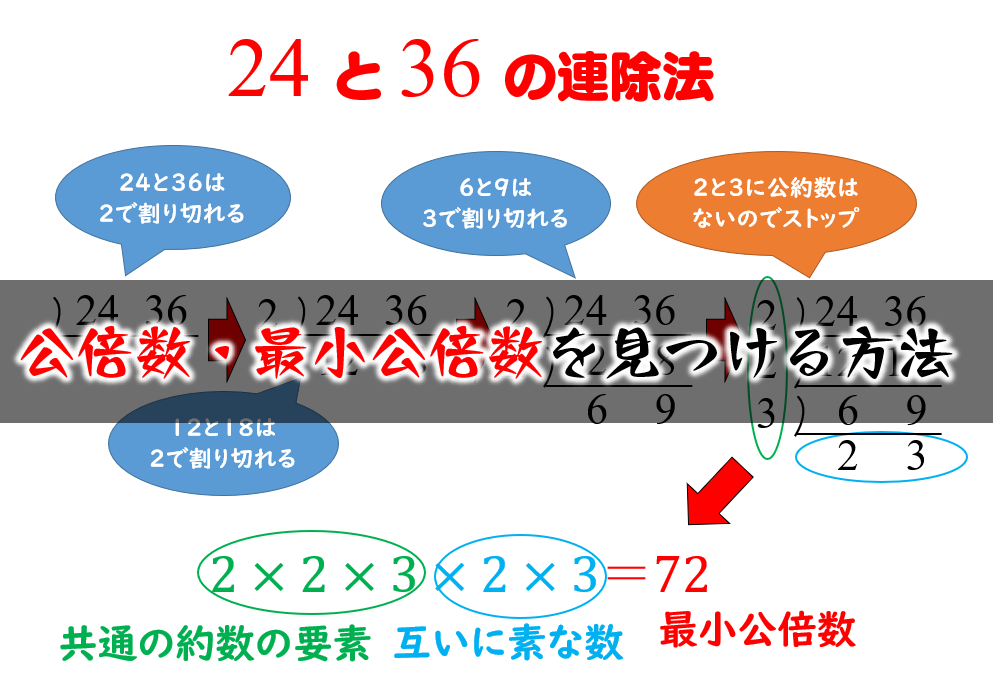



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




高校数学a 倍数の個数1 かつ または 練習編 映像授業のtry It トライイット
考公倍数の求め方を,公倍数の意味や性質などを基に考え,説明して いる。 技公倍数,最小公倍数を求めることができる。 4 ・3つの数の公倍数の求め方を理解する。 技3つの数の公倍数,最小公倍数を,数直線を活用するなどして求め ることができる。"被写界深度 DoF i "は"焦点深度 DoF o "を"縦倍率 α"で割る ことで求められます。 この式によると,Fナンバーが小さい(明るい)レンズ,画素ピッチの小さいセンサ,及び光学倍率が大きい(拡大)ほど被写界深度の幅は狭くなります。 最大公約数の求め方 最大公約数の求め方を2つ紹介します。 それは「すだれ算」と「ユークリッドの互除法」です。 求め方その① すだれ算 すだれ算では、まず最大公約数を求めたい数を横に並べて書きます。




1から100までの整数のうち3の倍数は何個 1から100までの整数のうち6の倍数は何個 1から100までの整数のうち2で割り切れるが3で割り切れない数は何個 ウルトラフリーダム




108 5 2 Descubre Como Resolverlo En Qanda
倍数 とは、ある数を2倍、3倍、4倍などと整数倍した数のことでしたよね。 例えば、6と15の最小公倍数を求める時は、それぞれの数の倍数を求めて、6の倍数(6、12、18、24、30)と15の倍数(15、30、45、60)で共通する一番小さい数を探せば最小公倍数は求まります。 答えは30になります。 しかしながら、このように計算すると計算間違えすることもよくあり時間も壁倍率と水平力・変形角の関係 壁量充足率の計算例 風圧力に対する必要壁量を求めるときの注意 見付面積の求め方 step1 地震力に対する必要壁量を求める。(各階ごとに算出) 公倍数、最小公倍数の意味と求め方を理解している。 4 最小公倍数を活用する具体的な場面を考え、公倍数あるいは最小公倍数についての理解を深める。 最小公倍数の考え方を、具体的な場面で活用している。 倍数や最小公倍数を求めることができる。 5




公約数 最大公約数 公倍数 最小公倍数 求め方 ぐらたん塾




これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ
ピタゴラス数とは ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たす自然数の組 ( a, b, c) (a,b,c) (a,b,c) をピタゴラス数と呼ぶ。 と補集合の個数を求めるときには「全体からくり抜く」 のが近道! つまり、 全体から5の倍数の個数を引く ことを考えればいいんだよ。 n(5の倍数でない数)=n(全体)n(5の倍数) だね。倍率=(250 ÷ ルーペの焦点距離)+1倍率=(ディオプター ÷ 4) +1焦点距離=1000 ÷ ディオプター 上記がルーペの倍率を表す計算式です。 例えば、焦点距離が100ミリのルーペは(250÷100)+1=3.5倍 と言う感じです。 ディオプターが4の場合(4÷4)+1




2 13の倍数の判定法をまとめ 簡単な倍数の見分け方
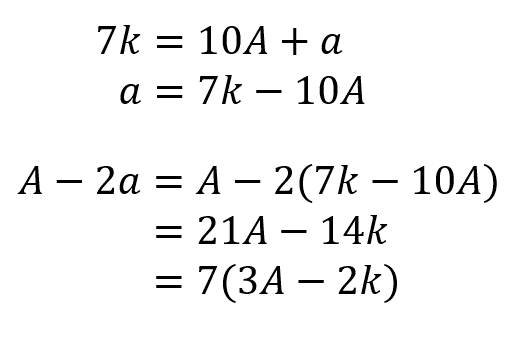



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ
なので、最小公約数と最大公倍数という言葉は使いません。 約数と倍数の発展① 最大公約数と最小公倍数の求め方(はしご算) 最大公約数と最小公倍数は、これまでのように小さい数から調べていくほかに、とても簡単な方法があります。



Studydoctor約数 倍数とは その求め方 Studydoctor




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook
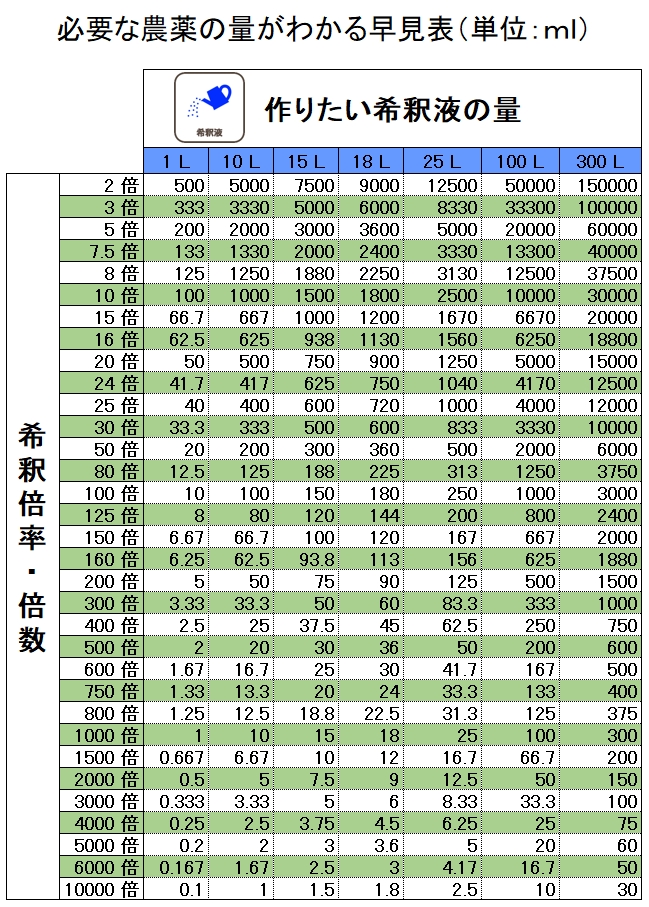



図解でわかる農薬の希釈倍率 倍数と早見表 計算方法と注意点も解説
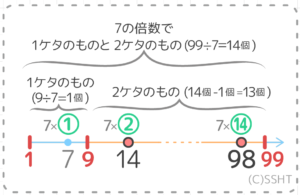



小学生 倍数の個数の求め方 2ケタ 3ケタ等 中学受験頻出 そうちゃ式 受験算数 新1号館



倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




11のかけ算 11の倍数 のわかりやすい計算方法 Irohabook




2 13の倍数の判定法をまとめ 簡単な倍数の見分け方




倍数の見つけ方を教えて下さい Clear




倍数判定法まとめ 3の倍数 4の倍数 7の倍数などの見分け方とは 遊ぶ数学



乙4危険物の指定数量の倍率計算を習得しよう Uhiyamabumi
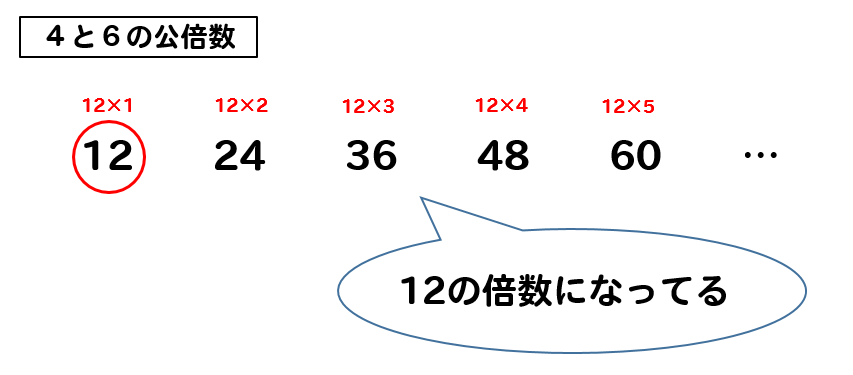



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




あなたの受験成長論 Twitterren 倍数の見分け方 各倍数 2 9 の見分け方について これを覚えておくと 約分するときなどに役立つ 7の 倍数の見分け方はちょっと難しい




小5 倍数の求め方 日本語版 Youtube




102 See How To Solve It At Qanda




数学 11の倍数の判定方法




プログラミング 数学 特定条件の数は何個 Scratch Yuyu Log




塾長ブログ 倍数の見つけ方
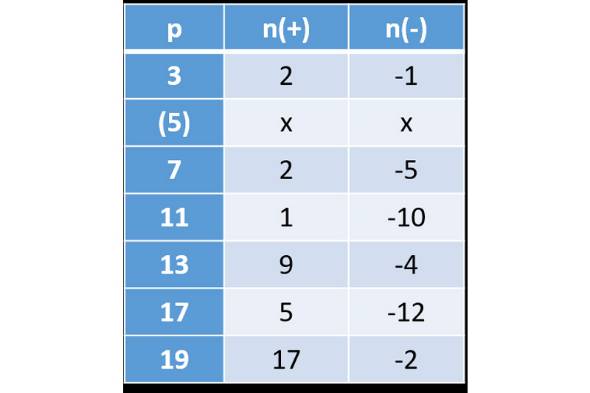



ある数が の倍数か を見分けるための 万能 な方法 ねとらぼ




知らないと受験で損をする 倍数の見分け方とその使い道
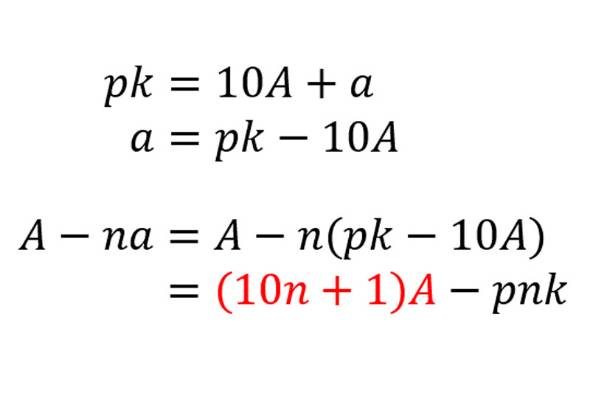



ある数が の倍数か を見分けるための 万能 な方法 ねとらぼ




指定数量ってなに 指定数量の倍数 図解でわかる危険物取扱者講座




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料
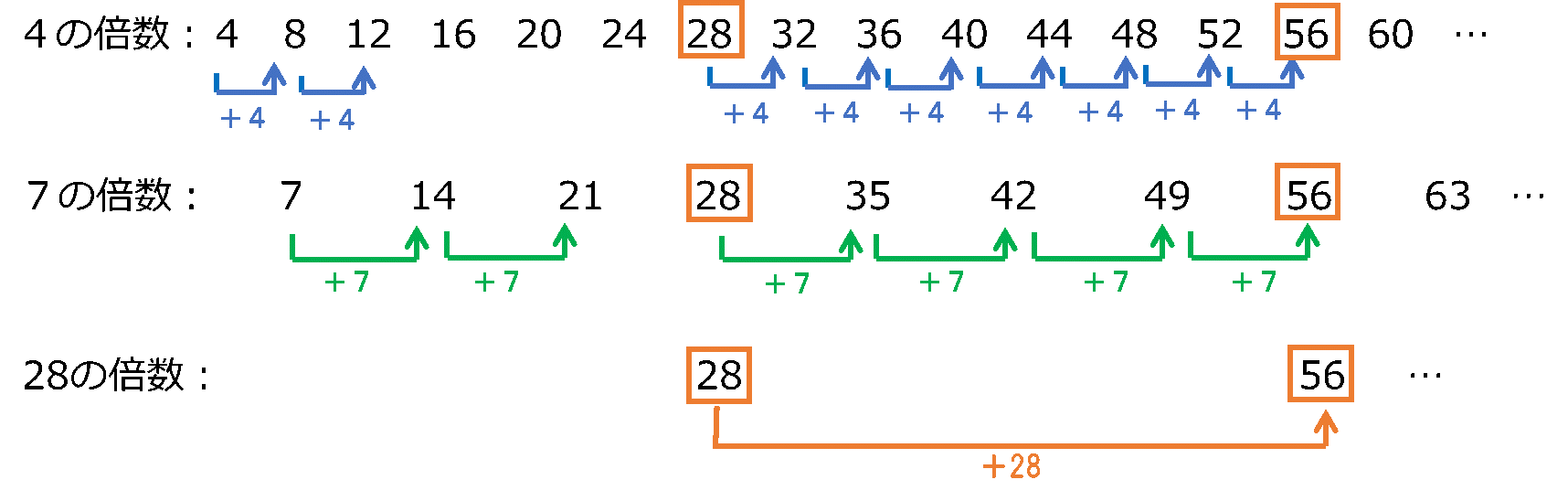



倍数と約数の教え方 5 倍数 公倍数の実践問題 ママのための受験算数の教え方プチ講座 中学受験ナビ




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



3




7の倍数判定法 Sakurai Susumu Website




倍数 公倍数の求め方 もう一度やり直しの算数 数学
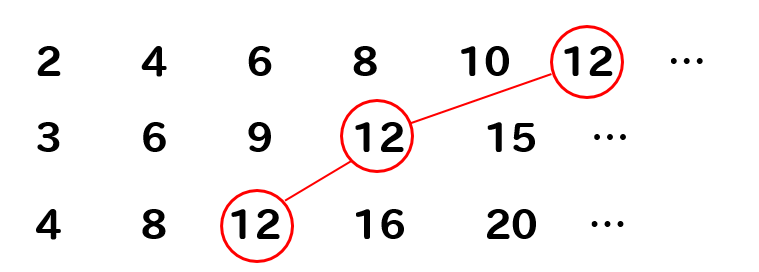



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




求め方を教えてください Clear



3




小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ



1




公約数 公倍数の求め方 Z Square Z会




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ




最小公倍数の求め方とは 数字が何個あっても計算できるやり方をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
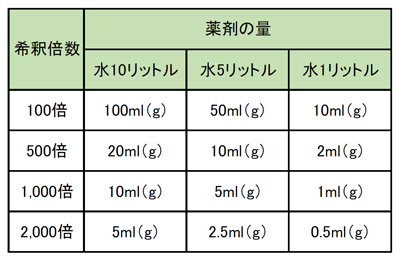



農薬の希釈 きしゃく 倍数とは Ja西春日井
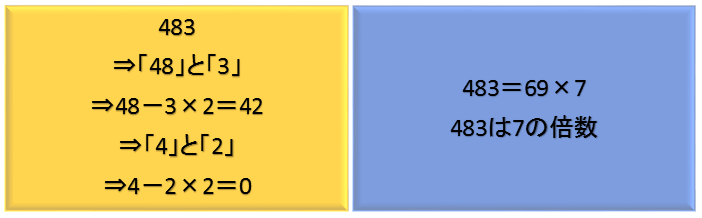



これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ




数学ia 整数を並べてできる3の倍数の個数を楽に求める方法 大学入試数学の考え方と解法




小5 算数 小5 倍数 公倍数 最小公倍数 Youtube




高校数学a 階乗の素因数の個数 階乗の末尾に連続して並ぶ0の個数 ルジャンドルの公式 受験の月




倍数とはどのような数ですか 用語の区別と最小公倍数の求め方に慣れよう 中学受験ナビ



5年算数整数 教え方のポイント
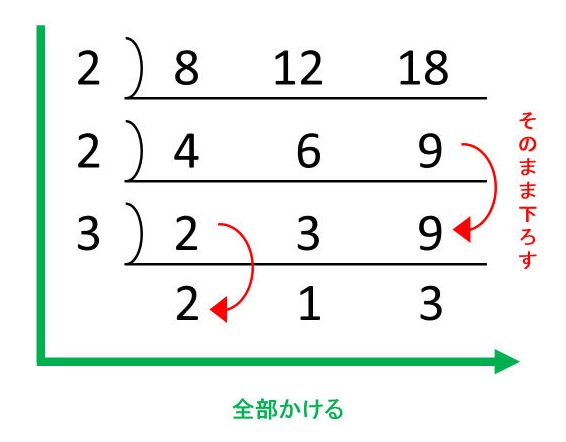



倍数とはどのような数ですか 用語の区別と最小公倍数の求め方に慣れよう 中学受験ナビ




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook




の倍数は何通りできるか問題 数学の偏差値を上げて合格を目指す
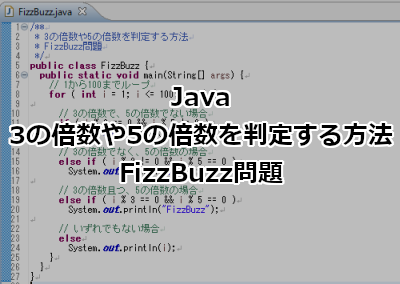



Java 3の倍数や5の倍数を判定する方法 Fizzbuzz問題 ホームページ制作のサカエン Developer S Blog




これなら簡単 7の倍数の見分け方は 2倍と引き算 にある 倍数判定法一覧 アタリマエ



倍数 公倍数 最小公倍数 通分 分数のたし算ひき算の授業 教材 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
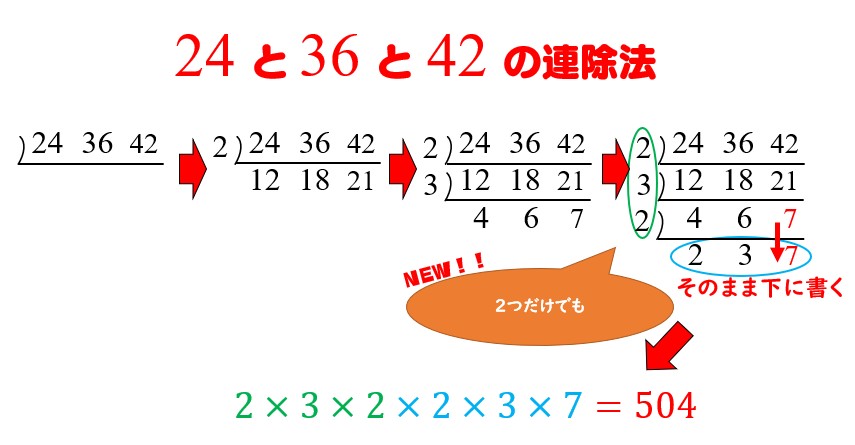



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun
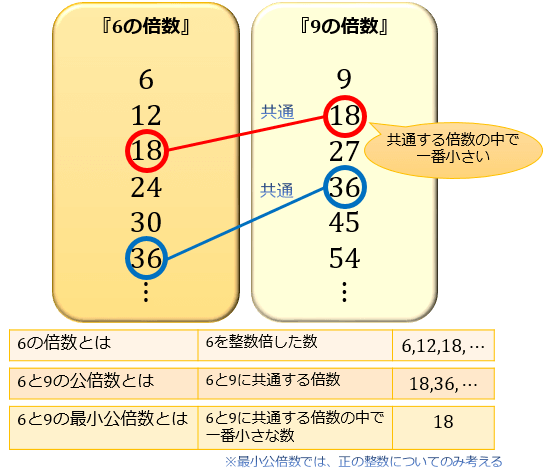



最小公倍数って何 その求め方と素因数分解のテクニック アタリマエ




小学校5年 算数 公倍数の求め方 Youtube




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料



2




24 2 A B A 56 B 48 2 Descubre Como Resolverlo En Qanda
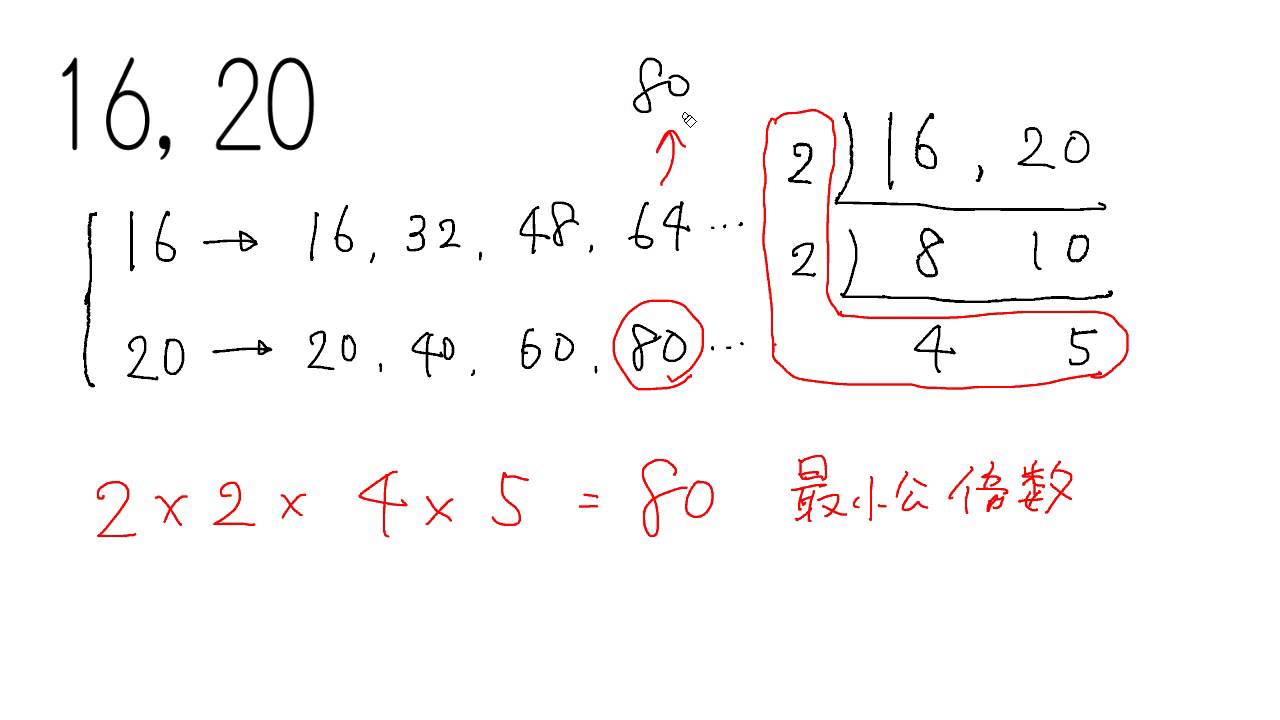



大きな数の最小公倍数の求め方 Youtube




知らないと受験で損をする 倍数の見分け方とその使い道




高校数学a 倍数の個数1 かつ または 映像授業のtry It トライイット




倍数と約数 倍数の個数 重要 算数の教え方教えますmother S Math Happy Study Support




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座
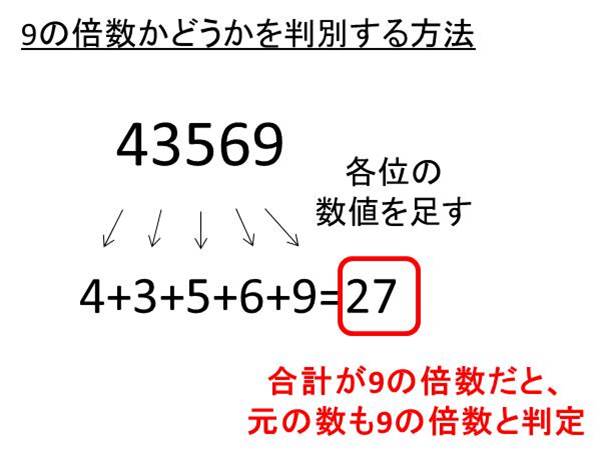



9の倍数の判別方法 各位の和から見分ける モッカイ




競プロ 素因数分解と約数と倍数 なかけんの数学ノート



約数 倍数



1




倍数とは 倍数の見分け方 ぐらたん塾




倍数 約数 の見つけ方 30代医学生のチャレンジ日誌 沖縄



約数 倍数




1からp Kまでの自然数のうち Pの倍数の個数の求め方を教えてください Clear




3の倍数の性質と見分け方 3の倍数早見表つき Irohabook




知らないと受験で損をする 倍数の見分け方とその使い道




Newみんなの算数講座6 倍数の判定法 中学受験の算数知恵宝庫




3桁の自然数の中で 次の個数を求めよ という問題なのですが 以下の 数学 教えて Goo



小学生算数 倍数と公倍数とは 見つけ方や見分け方を解説 数スタ




倍数判定法とは 恋する中学受験 大学受験を見据えた中学受験



倍数とはどのような数ですか 用語の区別と最小公倍数の求め方に慣れよう 中学受験ナビ




数学 整数 3の倍数 9の倍数の見分け方 理由 オンライン無料塾 ターンナップ Youtube




看護 予備校の講師が図解で基礎数学を簡単に説明 9の倍数から見つける問題 基礎講座23 Kazアカデミー 大阪の看護学校 看護予備校



数学 順列について 3の倍数の4桁を作るとき 各位の和が3の倍数 Yahoo 知恵袋




4の倍数かつ6の倍数 4の倍数であるが6の倍数でない数 5の倍数であるが7の倍数でない数 などの求め方 100以下の自然数 ウルトラフリーダム




エがわかりません どうやって考えてますか 総和の出し方がわかりません Clear




102 See How To Solve It At Qanda



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




倍数判定法まとめ 3の倍数 4の倍数 7の倍数などの見分け方とは 遊ぶ数学




倍数 約数 算数用語集
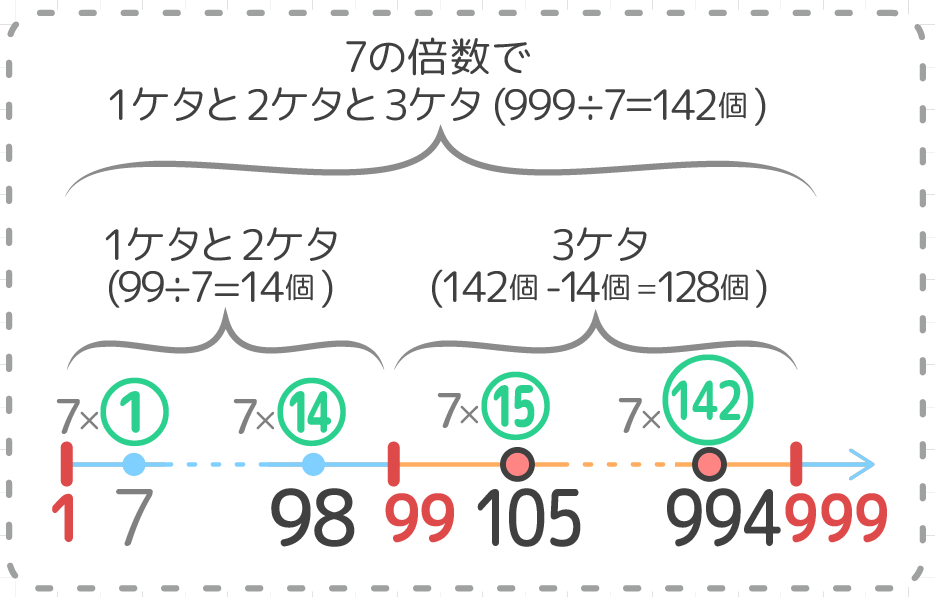



小学生 倍数の個数の求め方 2ケタ 3ケタ等 中学受験頻出 そうちゃ式 受験算数 新1号館




倍数と約数とは 大人の学び直し算数 計算のやり方解説 無料




5年の算数ソフト 倍数と約数 さくら社




整数7 倍数判定法5 11の倍数の判定法 怜悧玲瓏 高校数学を天空から俯瞰する




倍数の個数を求める問題 どうやって考えればいい 数スタ




小5 算数 小5 18 倍数と公倍数 Youtube




の倍数 を見分ける方法 全部に使える万能なやり方があるのだ




高校数学a 3の倍数 9の倍数の見分け方 映像授業のtry It トライイット




高校数学b 等差数列を利用する倍数の和 受験の月




高校数学a 4の倍数 8の倍数の見分け方 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿